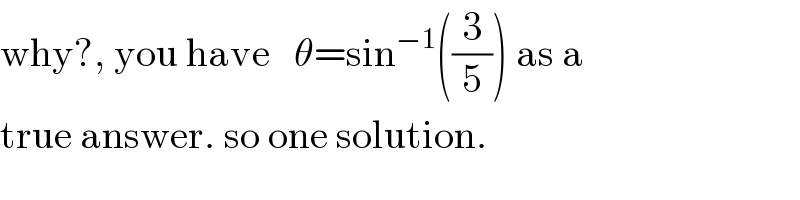Question Number 17095 by Tinkutara last updated on 30/Jun/17
![The total number of solutions of the equation tan x + sec x = 2 which lie in the interval [0, 2π] is](https://www.tinkutara.com/question/Q17095.png)
Answered by sma3l2996 last updated on 30/Jun/17
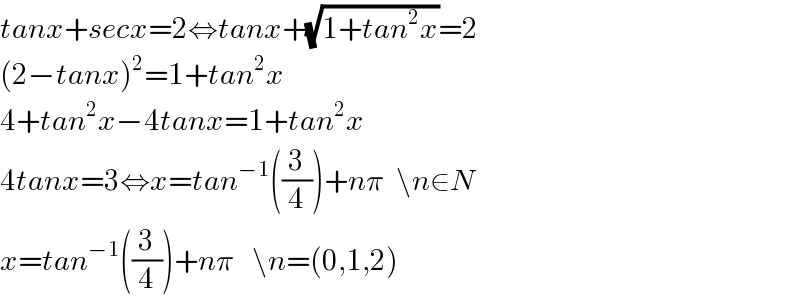
Commented by Tinkutara last updated on 01/Jul/17

Commented by ajfour last updated on 01/Jul/17
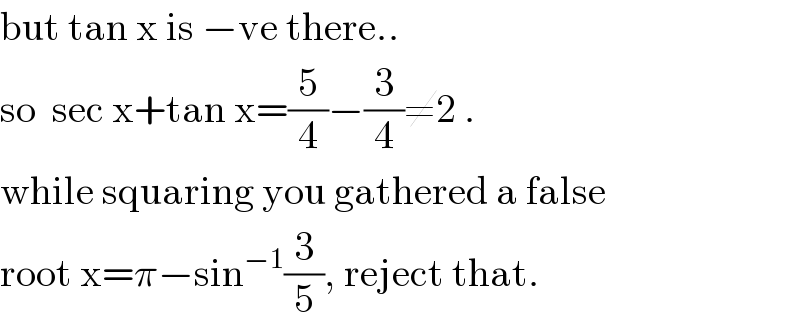
Commented by sma3l2996 last updated on 01/Jul/17
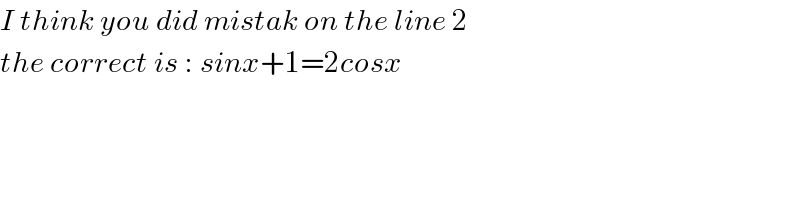
Commented by ajfour last updated on 01/Jul/17