the-value-of-2-n-is-

Question Number 155242 by aliyn last updated on 27/Sep/21

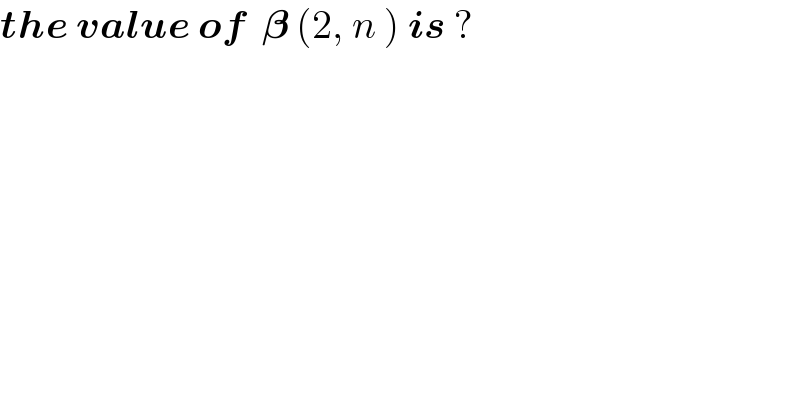
t h e v a l u e o f β (2, n) i s ?

Commented by tabata last updated on 27/Sep/21

= \frac{Γ 2 Γ (n)}{Γ (n + 2)} = \frac{(n - 1)!}{(n + 1)!} = \frac{(n - 1)!}{n (n + 1) (n - 1)!} = \frac{1}{n (n + 1)}

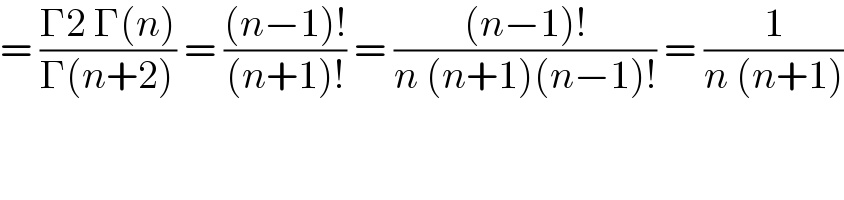
Answered by puissant last updated on 27/Sep/21

β (2, n) = \frac{Γ (2) Γ (n)}{Γ (n + 2)} = \frac{1 (n - 1)!}{(n + 1)!} = \frac{1}{n (n + 1)} . .

= \frac{1}{n} - \frac{1}{n + 1} . .

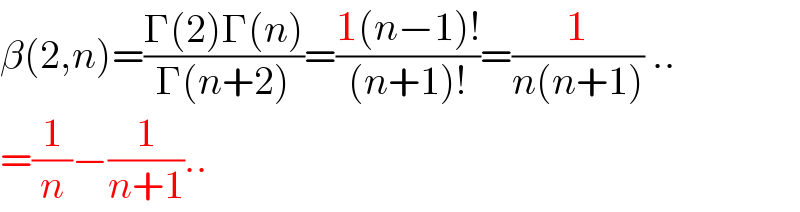
Commented by aliyn last updated on 27/Sep/21

s i r Γ 2 = Γ (1 + 1) = 1 \times 1! = 1 h o w Γ 2 = 2 ?

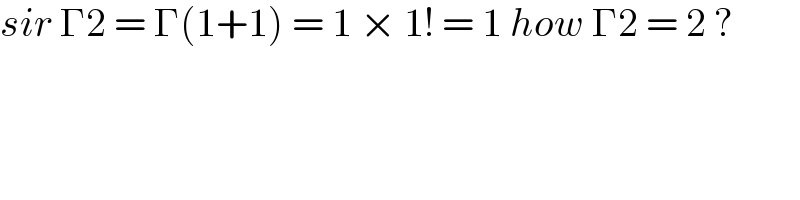
Commented by puissant last updated on 27/Sep/21

T h a n k s . .