Menu Close

The-value-of-3-20-14-2-3-20-14-2-is-

Tinku Tara 0 Comments
Pin




Question Number 43793 by gunawan last updated on 15/Sep/18
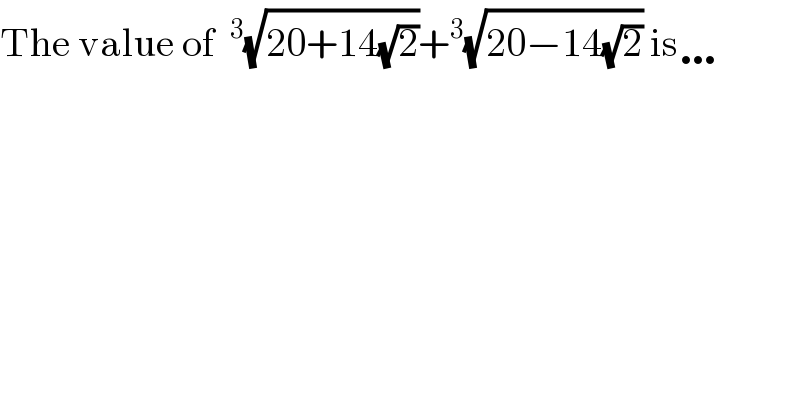
The value of ^3 (√(20+14(√2)))+^3 (√(20−14(√2))) is…
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\:^{\mathrm{3}} \sqrt{\mathrm{20}+\mathrm{14}\sqrt{\mathrm{2}}}+^{\mathrm{3}} \sqrt{\mathrm{20}−\mathrm{14}\sqrt{\mathrm{2}}}\:\mathrm{is}\ldots \\ $$
Answered by Joel578 last updated on 15/Sep/18
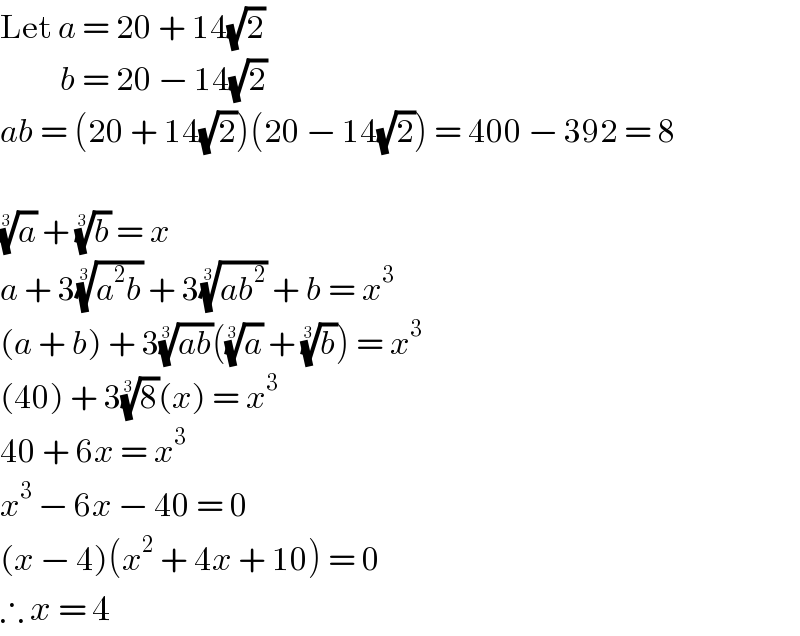
Let a = 20 + 14(√2) b = 20 − 14(√2) ab = (20 + 14(√2))(20 − 14(√2)) = 400 − 392 = 8 (a)^(1/3) + (b)^(1/3) = x a + 3((a^2 b))^(1/3) + 3((ab^2 ))^(1/3) + b = x^3 (a + b) + 3((ab))^(1/3) ((a)^(1/3) + (b)^(1/3) ) = x^3 (40) + 3(8)^(1/3) (x) = x^3 40 + 6x = x^3 x^3 − 6x − 40 = 0 (x − 4)(x^2 + 4x + 10) = 0 ∴ x = 4
$$\mathrm{Let}\:{a}\:=\:\mathrm{20}\:+\:\mathrm{14}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{b}\:=\:\mathrm{20}\:−\:\mathrm{14}\sqrt{\mathrm{2}} \\ $$$${ab}\:=\:\left(\mathrm{20}\:+\:\mathrm{14}\sqrt{\mathrm{2}}\right)\left(\mathrm{20}\:−\:\mathrm{14}\sqrt{\mathrm{2}}\right)\:=\:\mathrm{400}\:−\:\mathrm{392}\:=\:\mathrm{8} \\ $$$$ \\ $$$$\sqrt[{\mathrm{3}}]{{a}}\:+\:\sqrt[{\mathrm{3}}]{{b}}\:=\:{x} \\ $$$${a}\:+\:\mathrm{3}\sqrt[{\mathrm{3}}]{{a}^{\mathrm{2}} {b}}\:+\:\mathrm{3}\sqrt[{\mathrm{3}}]{{ab}^{\mathrm{2}} }\:+\:{b}\:=\:{x}^{\mathrm{3}} \\ $$$$\left({a}\:+\:{b}\right)\:+\:\mathrm{3}\sqrt[{\mathrm{3}}]{{ab}}\left(\sqrt[{\mathrm{3}}]{{a}}\:+\:\sqrt[{\mathrm{3}}]{{b}}\right)\:=\:{x}^{\mathrm{3}} \\ $$$$\left(\mathrm{40}\right)\:+\:\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{8}}\left({x}\right)\:=\:{x}^{\mathrm{3}} \\ $$$$\mathrm{40}\:+\:\mathrm{6}{x}\:=\:{x}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} \:−\:\mathrm{6}{x}\:−\:\mathrm{40}\:=\:\mathrm{0} \\ $$$$\left({x}\:−\:\mathrm{4}\right)\left({x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:+\:\mathrm{10}\right)\:=\:\mathrm{0} \\ $$$$\therefore\:{x}\:=\:\mathrm{4}\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Sep/18
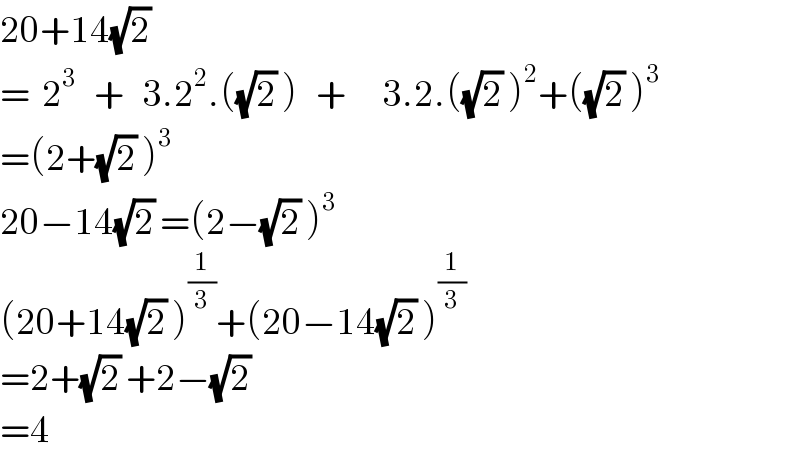
20+14(√2) = 2^3 + 3.2^2 .((√2) ) + 3.2.((√2) )^2 +((√2) )^3 =(2+(√2) )^3 20−14(√2) =(2−(√2) )^3 (20+14(√2) )^(1/3) +(20−14(√2) )^(1/3) =2+(√2) +2−(√2) =4
$$\mathrm{20}+\mathrm{14}\sqrt{\mathrm{2}}\: \\ $$$$=\:\:\mathrm{2}^{\mathrm{3}} \:\:\:+\:\:\:\mathrm{3}.\mathrm{2}^{\mathrm{2}} .\left(\sqrt{\mathrm{2}}\:\right)\:\:\:+\:\:\:\:\:\:\mathrm{3}.\mathrm{2}.\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{2}+\sqrt{\mathrm{2}}\:\right)^{\mathrm{3}} \\ $$$$\mathrm{20}−\mathrm{14}\sqrt{\mathrm{2}}\:=\left(\mathrm{2}−\sqrt{\mathrm{2}}\:\right)^{\mathrm{3}} \\ $$$$\left(\mathrm{20}+\mathrm{14}\sqrt{\mathrm{2}}\:\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\mathrm{20}−\mathrm{14}\sqrt{\mathrm{2}}\:\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\mathrm{2}+\sqrt{\mathrm{2}}\:+\mathrm{2}−\sqrt{\mathrm{2}}\: \\ $$$$=\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *