Question Number 97512 by bemath last updated on 08/Jun/20
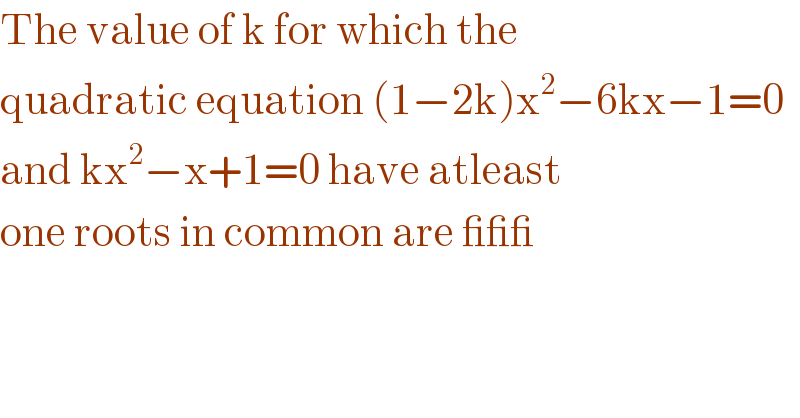
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{k}\:\mathrm{for}\:\mathrm{which}\:\mathrm{the} \\ $$$$\mathrm{quadratic}\:\mathrm{equation}\:\left(\mathrm{1}−\mathrm{2k}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{6kx}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{kx}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\:\mathrm{have}\:\mathrm{atleast} \\ $$$$\mathrm{one}\:\mathrm{roots}\:\mathrm{in}\:\mathrm{common}\:\mathrm{are}\:\_\_\_ \\ $$
Commented by john santu last updated on 08/Jun/20
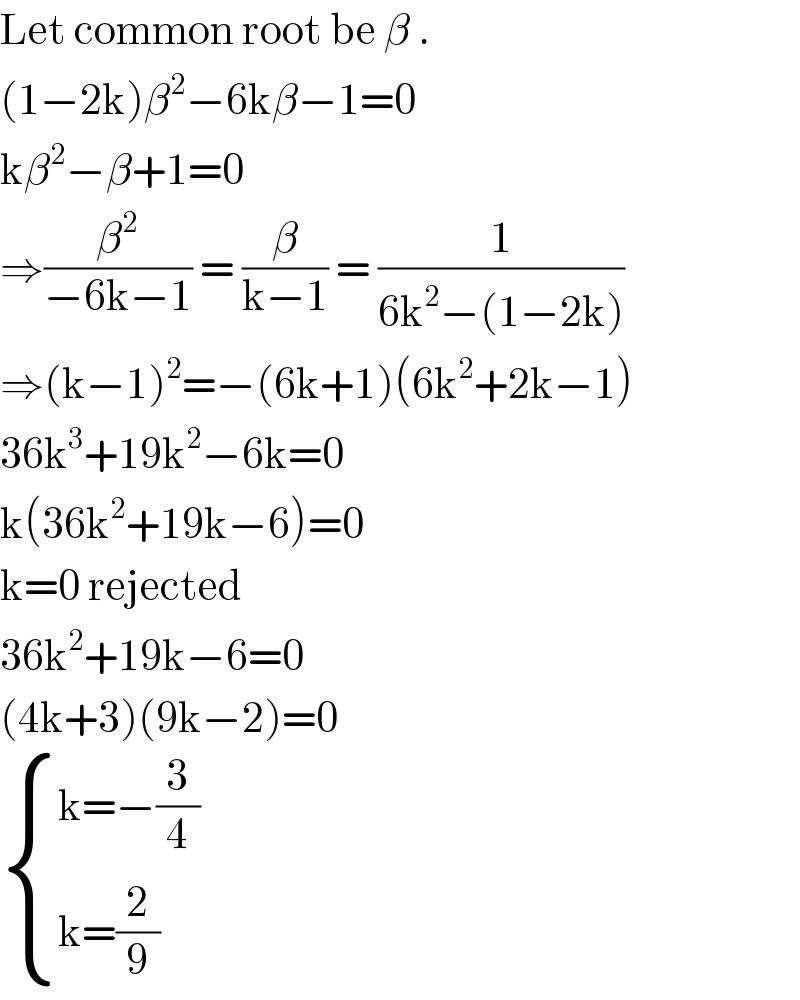
$$\mathrm{Let}\:\mathrm{common}\:\mathrm{root}\:\mathrm{be}\:\beta\:. \\ $$$$\left(\mathrm{1}−\mathrm{2k}\right)\beta^{\mathrm{2}} −\mathrm{6k}\beta−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{k}\beta^{\mathrm{2}} −\beta+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\frac{\beta^{\mathrm{2}} }{−\mathrm{6k}−\mathrm{1}}\:=\:\frac{\beta}{\mathrm{k}−\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{6k}^{\mathrm{2}} −\left(\mathrm{1}−\mathrm{2k}\right)} \\ $$$$\Rightarrow\left(\mathrm{k}−\mathrm{1}\right)^{\mathrm{2}} =−\left(\mathrm{6k}+\mathrm{1}\right)\left(\mathrm{6k}^{\mathrm{2}} +\mathrm{2k}−\mathrm{1}\right) \\ $$$$\mathrm{36k}^{\mathrm{3}} +\mathrm{19k}^{\mathrm{2}} −\mathrm{6k}=\mathrm{0} \\ $$$$\mathrm{k}\left(\mathrm{36k}^{\mathrm{2}} +\mathrm{19k}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\mathrm{k}=\mathrm{0}\:\mathrm{rejected} \\ $$$$\mathrm{36k}^{\mathrm{2}} +\mathrm{19k}−\mathrm{6}=\mathrm{0} \\ $$$$\left(\mathrm{4k}+\mathrm{3}\right)\left(\mathrm{9k}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{k}=−\frac{\mathrm{3}}{\mathrm{4}}}\\{\mathrm{k}=\frac{\mathrm{2}}{\mathrm{9}}}\end{cases} \\ $$
Commented by bemath last updated on 08/Jun/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
