Question Number 39384 by rahul 19 last updated on 05/Jul/18
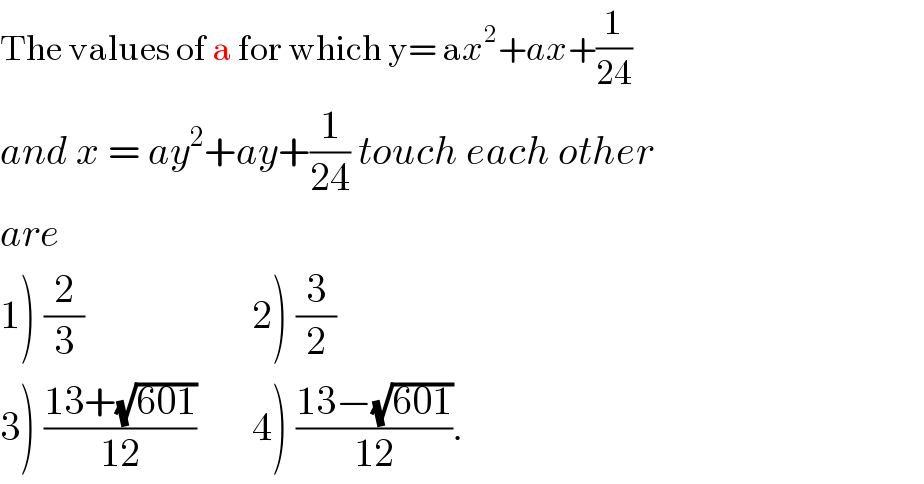
$$\mathrm{The}\:\mathrm{values}\:\mathrm{of}\:\mathrm{a}\:\mathrm{for}\:\mathrm{which}\:\mathrm{y}=\:\mathrm{a}{x}^{\mathrm{2}} +{ax}+\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${and}\:{x}\:=\:{ay}^{\mathrm{2}} +{ay}+\frac{\mathrm{1}}{\mathrm{24}}\:{touch}\:{each}\:{other} \\ $$$${are} \\ $$$$\left.\mathrm{1}\left.\right)\:\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\right)\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left.\mathrm{3}\left.\right)\:\frac{\mathrm{13}+\sqrt{\mathrm{601}}}{\mathrm{12}}\:\:\:\:\:\:\:\mathrm{4}\right)\:\frac{\mathrm{13}−\sqrt{\mathrm{601}}}{\mathrm{12}}. \\ $$
Answered by ajfour last updated on 05/Jul/18
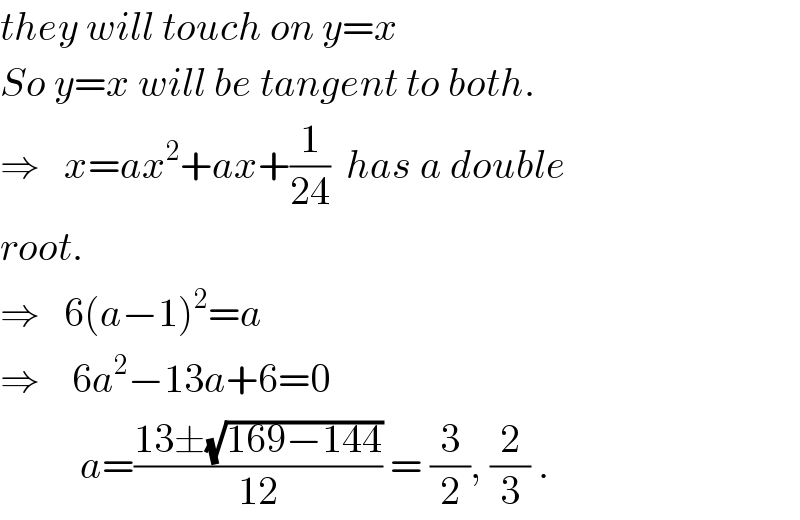
$${they}\:{will}\:{touch}\:{on}\:{y}={x} \\ $$$${So}\:{y}={x}\:{will}\:{be}\:{tangent}\:{to}\:{both}. \\ $$$$\Rightarrow\:\:\:{x}={ax}^{\mathrm{2}} +{ax}+\frac{\mathrm{1}}{\mathrm{24}}\:\:{has}\:{a}\:{double} \\ $$$${root}. \\ $$$$\Rightarrow\:\:\:\mathrm{6}\left({a}−\mathrm{1}\right)^{\mathrm{2}} ={a} \\ $$$$\Rightarrow\:\:\:\:\mathrm{6}{a}^{\mathrm{2}} −\mathrm{13}{a}+\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}=\frac{\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{144}}}{\mathrm{12}}\:=\:\frac{\mathrm{3}}{\mathrm{2}},\:\frac{\mathrm{2}}{\mathrm{3}}\:. \\ $$
Commented by MJS last updated on 05/Jul/18

$$\mathrm{master}\:\mathrm{you}'\mathrm{ve}\:\mathrm{been}\:\mathrm{faster}… \\ $$
Commented by rahul 19 last updated on 06/Jul/18
Thank you sir!
Answered by MJS last updated on 05/Jul/18

$$“\mathrm{touching}''\:\mathrm{means}\:\mathrm{only}\:\mathrm{1}\:\mathrm{intersection}\:\mathrm{point} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} +{ax}+\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right):\:{x}={ay}^{\mathrm{2}} +{ay}+\frac{\mathrm{1}}{\mathrm{24}} \\ $$$$\mathrm{so}\:\mathrm{they}\:\mathrm{must}\:\mathrm{have}\:\mathrm{the}\:\mathrm{common}\:\mathrm{tangent}\:{y}={x} \\ $$$${ax}^{\mathrm{2}} +\left({a}−\mathrm{1}\right){x}+\frac{\mathrm{1}}{\mathrm{24}}=\mathrm{0}\:\mathrm{must}\:\mathrm{have}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{solution}\:\Rightarrow \\ $$$$\Rightarrow\:{B}^{\mathrm{2}} −\mathrm{4}{AC}=\mathrm{0}\:\Rightarrow\:\left({a}−\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{6}}{a}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} −\frac{\mathrm{13}}{\mathrm{6}}{a}+\mathrm{1}=\mathrm{0} \\ $$$${o}=\frac{\mathrm{13}}{\mathrm{12}}\pm\frac{\mathrm{5}}{\mathrm{12}} \\ $$$${a}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}};\:{a}_{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 06/Jul/18
Thank you sir!
