Question Number 21071 by Tinkutara last updated on 12/Sep/17
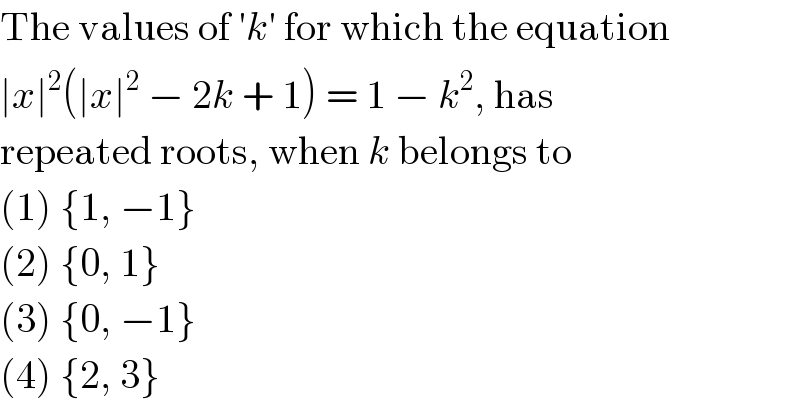
$$\mathrm{The}\:\mathrm{values}\:\mathrm{of}\:'{k}'\:\mathrm{for}\:\mathrm{which}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mid{x}\mid^{\mathrm{2}} \left(\mid{x}\mid^{\mathrm{2}} \:−\:\mathrm{2}{k}\:+\:\mathrm{1}\right)\:=\:\mathrm{1}\:−\:{k}^{\mathrm{2}} ,\:\mathrm{has} \\ $$$$\mathrm{repeated}\:\mathrm{roots},\:\mathrm{when}\:{k}\:\mathrm{belongs}\:\mathrm{to} \\ $$$$\left(\mathrm{1}\right)\:\left\{\mathrm{1},\:−\mathrm{1}\right\} \\ $$$$\left(\mathrm{2}\right)\:\left\{\mathrm{0},\:\mathrm{1}\right\} \\ $$$$\left(\mathrm{3}\right)\:\left\{\mathrm{0},\:−\mathrm{1}\right\} \\ $$$$\left(\mathrm{4}\right)\:\left\{\mathrm{2},\:\mathrm{3}\right\} \\ $$
Answered by mrW1 last updated on 13/Sep/17
![let u=∣x∣^2 ⇒u(u−2k+1)=1−k^2 ⇒u^2 −(2k−1)u+(k^2 −1)=0 ⇒u=((2k−1±(√((2k−1)^2 −4(k^2 −1))))/2) ⇒u=∣x∣^2 =((2k−1±(√(5−4k)))/2)≥0 5−4k≥0 ⇒k≤(5/4)=1.25 ...(1) 2k−1+(√(5−4k))≥0 ⇒k≥−1 ...(2) 2k−1−(√(5−4k))≥0 ⇒k≥1 ...(3) (1)+(2)+(3)⇒k∈[1,(5/4)] ???](https://www.tinkutara.com/question/Q21127.png)
$$\mathrm{let}\:\mathrm{u}=\mid\mathrm{x}\mid^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{u}\left(\mathrm{u}−\mathrm{2k}+\mathrm{1}\right)=\mathrm{1}−\mathrm{k}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{u}^{\mathrm{2}} −\left(\mathrm{2k}−\mathrm{1}\right)\mathrm{u}+\left(\mathrm{k}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{u}=\frac{\mathrm{2k}−\mathrm{1}\pm\sqrt{\left(\mathrm{2k}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{k}^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{u}=\mid\mathrm{x}\mid^{\mathrm{2}} =\frac{\mathrm{2k}−\mathrm{1}\pm\sqrt{\mathrm{5}−\mathrm{4k}}}{\mathrm{2}}\geqslant\mathrm{0} \\ $$$$\mathrm{5}−\mathrm{4k}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{k}\leqslant\frac{\mathrm{5}}{\mathrm{4}}=\mathrm{1}.\mathrm{25}\:\:\:…\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{2k}−\mathrm{1}+\sqrt{\mathrm{5}−\mathrm{4k}}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{k}\geqslant−\mathrm{1}\:\:\:…\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{2k}−\mathrm{1}−\sqrt{\mathrm{5}−\mathrm{4k}}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{k}\geqslant\mathrm{1}\:\:\:…\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)+\left(\mathrm{3}\right)\Rightarrow\mathrm{k}\in\left[\mathrm{1},\frac{\mathrm{5}}{\mathrm{4}}\right] \\ $$$$??? \\ $$
Answered by Tinkutara last updated on 15/Sep/17
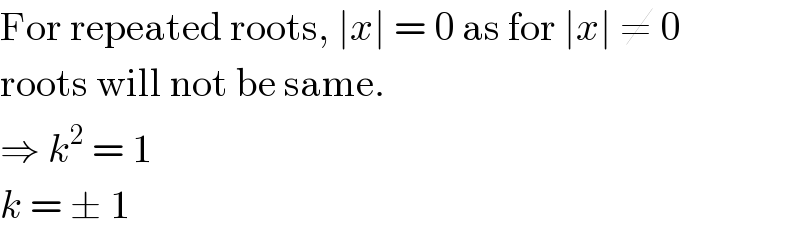
$$\mathrm{For}\:\mathrm{repeated}\:\mathrm{roots},\:\mid{x}\mid\:=\:\mathrm{0}\:\mathrm{as}\:\mathrm{for}\:\mid{x}\mid\:\neq\:\mathrm{0} \\ $$$$\mathrm{roots}\:\mathrm{will}\:\mathrm{not}\:\mathrm{be}\:\mathrm{same}. \\ $$$$\Rightarrow\:{k}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$${k}\:=\:\pm\:\mathrm{1} \\ $$
