Question Number 111006 by pete last updated on 01/Sep/20
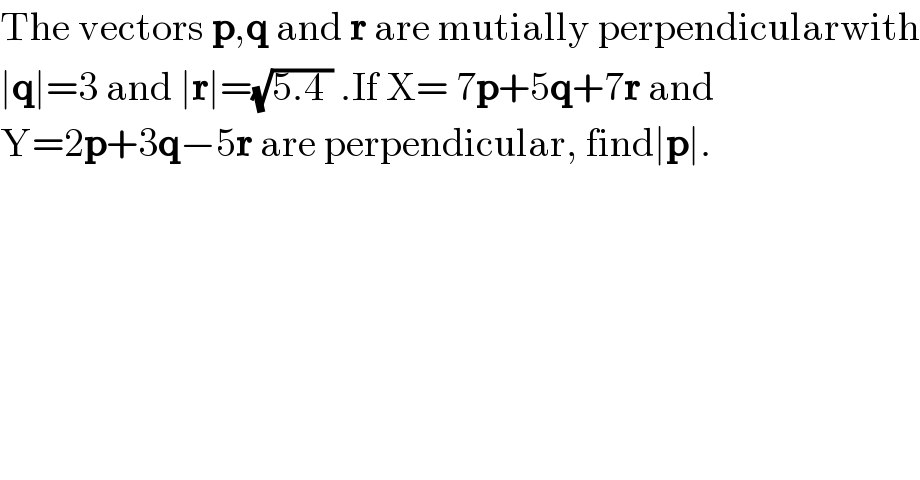
$$\mathrm{The}\:\mathrm{vectors}\:\boldsymbol{\mathrm{p}},\boldsymbol{\mathrm{q}}\:\mathrm{and}\:\boldsymbol{\mathrm{r}}\:\mathrm{are}\:\mathrm{mutially}\:\mathrm{perpendicularwith} \\ $$$$\mid\boldsymbol{\mathrm{q}}\mid=\mathrm{3}\:\mathrm{and}\:\mid\boldsymbol{\mathrm{r}}\mid=\sqrt{\mathrm{5}.\mathrm{4}\:}\:.\mathrm{If}\:\mathrm{X}=\:\mathrm{7}\boldsymbol{\mathrm{p}}+\mathrm{5}\boldsymbol{\mathrm{q}}+\mathrm{7}\boldsymbol{\mathrm{r}}\:\mathrm{and} \\ $$$$\mathrm{Y}=\mathrm{2}\boldsymbol{\mathrm{p}}+\mathrm{3}\boldsymbol{\mathrm{q}}−\mathrm{5}\boldsymbol{\mathrm{r}}\:\mathrm{are}\:\mathrm{perpendicular},\:\mathrm{find}\mid\boldsymbol{\mathrm{p}}\mid. \\ $$
Commented by kaivan.ahmadi last updated on 01/Sep/20
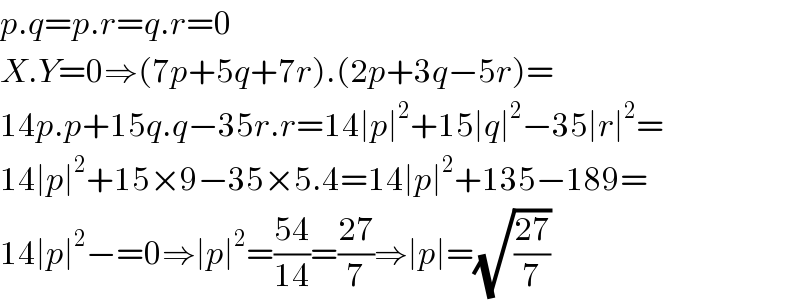
$${p}.{q}={p}.{r}={q}.{r}=\mathrm{0} \\ $$$${X}.{Y}=\mathrm{0}\Rightarrow\left(\mathrm{7}{p}+\mathrm{5}{q}+\mathrm{7}{r}\right).\left(\mathrm{2}{p}+\mathrm{3}{q}−\mathrm{5}{r}\right)= \\ $$$$\mathrm{14}{p}.{p}+\mathrm{15}{q}.{q}−\mathrm{35}{r}.{r}=\mathrm{14}\mid{p}\mid^{\mathrm{2}} +\mathrm{15}\mid{q}\mid^{\mathrm{2}} −\mathrm{35}\mid{r}\mid^{\mathrm{2}} = \\ $$$$\mathrm{14}\mid{p}\mid^{\mathrm{2}} +\mathrm{15}×\mathrm{9}−\mathrm{35}×\mathrm{5}.\mathrm{4}=\mathrm{14}\mid{p}\mid^{\mathrm{2}} +\mathrm{135}−\mathrm{189}= \\ $$$$\mathrm{14}\mid{p}\mid^{\mathrm{2}} −=\mathrm{0}\Rightarrow\mid{p}\mid^{\mathrm{2}} =\frac{\mathrm{54}}{\mathrm{14}}=\frac{\mathrm{27}}{\mathrm{7}}\Rightarrow\mid{p}\mid=\sqrt{\frac{\mathrm{27}}{\mathrm{7}}} \\ $$
Commented by pete last updated on 01/Sep/20
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir} \\ $$
