Menu Close

There-are-m-points-on-the-line-AB-and-n-points-on-the-line-AC-excluding-the-point-A-Triangles-are-formed-joining-these-points-i-When-point-A-is-not-included-ii-When-point-A-is-included-The-rat

Tinku Tara 0 Comments
Pin




Question Number 21760 by Tinkutara last updated on 03/Oct/17
There are m points on the line AB and n points on the line AC, excluding the point A. Triangles are formed joining these points (i) When point A is not included, (ii) When point A is included. The ratio of the number of such triangles is
$$\mathrm{There}\:\mathrm{are}\:{m}\:\mathrm{points}\:\mathrm{on}\:\mathrm{the}\:\mathrm{line}\:{AB}\:\mathrm{and} \\ $$$${n}\:\mathrm{points}\:\mathrm{on}\:\mathrm{the}\:\mathrm{line}\:{AC},\:\mathrm{excluding}\:\mathrm{the} \\ $$$$\mathrm{point}\:{A}.\:\mathrm{Triangles}\:\mathrm{are}\:\mathrm{formed}\:\mathrm{joining} \\ $$$$\mathrm{these}\:\mathrm{points} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{When}\:\mathrm{point}\:{A}\:\mathrm{is}\:\mathrm{not}\:\mathrm{included}, \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{When}\:\mathrm{point}\:{A}\:\mathrm{is}\:\mathrm{included}. \\ $$$$\mathrm{The}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{such}\:\mathrm{triangles} \\ $$$$\mathrm{is} \\ $$
Answered by mrW1 last updated on 03/Oct/17
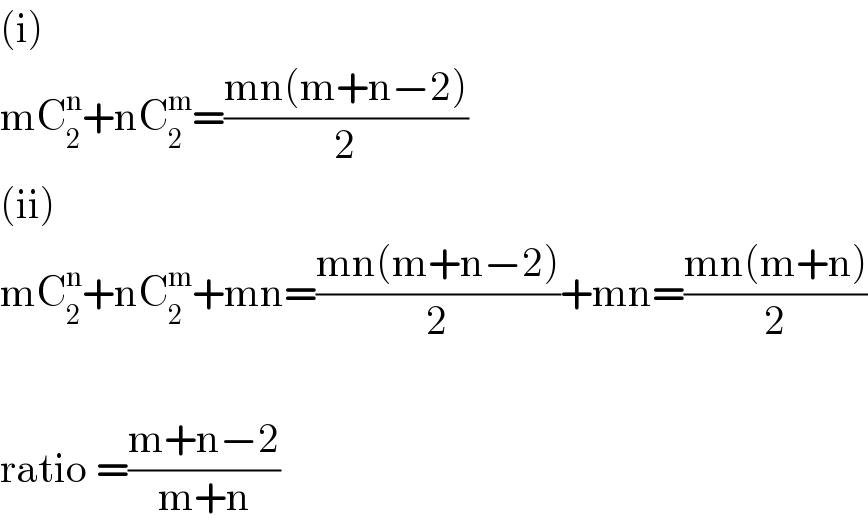
(i) mC_2 ^n +nC_2 ^m =((mn(m+n−2))/2) (ii) mC_2 ^n +nC_2 ^m +mn=((mn(m+n−2))/2)+mn=((mn(m+n))/2) ratio =((m+n−2)/(m+n))
$$\left(\mathrm{i}\right) \\ $$$$\mathrm{mC}_{\mathrm{2}} ^{\mathrm{n}} +\mathrm{nC}_{\mathrm{2}} ^{\mathrm{m}} =\frac{\mathrm{mn}\left(\mathrm{m}+\mathrm{n}−\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\left(\mathrm{ii}\right) \\ $$$$\mathrm{mC}_{\mathrm{2}} ^{\mathrm{n}} +\mathrm{nC}_{\mathrm{2}} ^{\mathrm{m}} +\mathrm{mn}=\frac{\mathrm{mn}\left(\mathrm{m}+\mathrm{n}−\mathrm{2}\right)}{\mathrm{2}}+\mathrm{mn}=\frac{\mathrm{mn}\left(\mathrm{m}+\mathrm{n}\right)}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{ratio}\:=\frac{\mathrm{m}+\mathrm{n}−\mathrm{2}}{\mathrm{m}+\mathrm{n}} \\ $$
Commented by Tinkutara last updated on 03/Oct/17
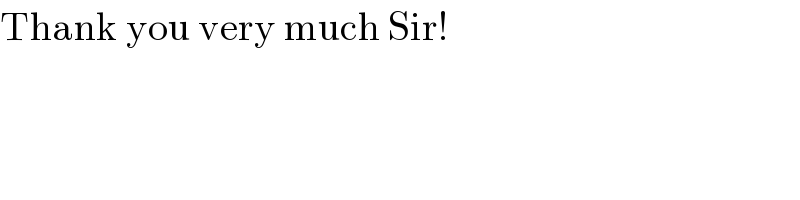
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by mrW1 last updated on 03/Oct/17
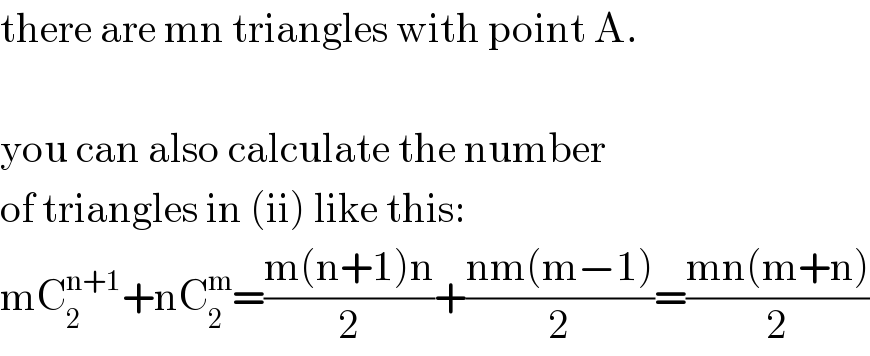
there are mn triangles with point A. you can also calculate the number of triangles in (ii) like this: mC_2 ^(n+1) +nC_2 ^m =((m(n+1)n)/2)+((nm(m−1))/2)=((mn(m+n))/2)
$$\mathrm{there}\:\mathrm{are}\:\mathrm{mn}\:\mathrm{triangles}\:\mathrm{with}\:\mathrm{point}\:\mathrm{A}. \\ $$$$ \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{also}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{number} \\ $$$$\mathrm{of}\:\mathrm{triangles}\:\mathrm{in}\:\left(\mathrm{ii}\right)\:\mathrm{like}\:\mathrm{this}: \\ $$$$\mathrm{mC}_{\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} +\mathrm{nC}_{\mathrm{2}} ^{\mathrm{m}} =\frac{\mathrm{m}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{n}}{\mathrm{2}}+\frac{\mathrm{nm}\left(\mathrm{m}−\mathrm{1}\right)}{\mathrm{2}}=\frac{\mathrm{mn}\left(\mathrm{m}+\mathrm{n}\right)}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *