Question Number 62587 by Jmasanja last updated on 23/Jun/19

$${three}\:{forces}\:{having}\:{equal}\:{magnitude} \\ $$$${s}\:{of}\:\mathrm{10}{N},\mathrm{20}{N}\:{and}\:\mathrm{30}{N}\:{make}\:{angles}\: \\ $$$${of}\:\mathrm{30}°,\mathrm{120}°\:{and}\:\mathrm{210}°\:{respectively}\:{with} \\ $$$${the}\:{positive}\:{direction}\:{of}\:{the}\:{x}\:{axis}. \\ $$$${By}\:{scale}\:{drawing}\:{find}\:{the}\:{magnitude} \\ $$$${and}\:{the}\:{direction}\:{of}\:{the}\:{resultant}\: \\ $$$${force} \\ $$
Commented by MJS last updated on 23/Jun/19
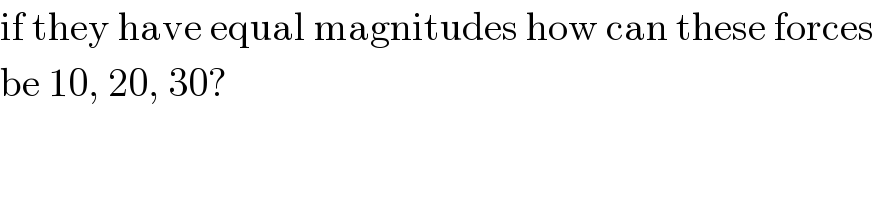
$$\mathrm{if}\:\mathrm{they}\:\mathrm{have}\:\mathrm{equal}\:\mathrm{magnitudes}\:\mathrm{how}\:\mathrm{can}\:\mathrm{these}\:\mathrm{forces} \\ $$$$\mathrm{be}\:\mathrm{10},\:\mathrm{20},\:\mathrm{30}? \\ $$
Answered by MJS last updated on 23/Jun/19
![F_1 =f_1 (((cos 30°)),((sin 30°)) )=f_1 ((((√3)/2)),((1/2)) ) F_2 =f_2 (((cos 120°)),((sin 120°)) )=f_2 (((−(1/2))),(((√3)/2)) ) F_3 =f_3 (((cos 210°)),((sin 210°)) )=f_3 (((−((√3)/2))),((−(1/2))) ) F_1 +F_2 +F_3 =(1/2) ((((√3)f_1 −f_2 −(√3)f_3 )),((f_1 +(√3)f_2 −f_3 )) )= [if f_1 =f_2 =f_3 =f] =(f/2) ((1),((√3)) )](https://www.tinkutara.com/question/Q62601.png)
$${F}_{\mathrm{1}} ={f}_{\mathrm{1}} \begin{pmatrix}{\mathrm{cos}\:\mathrm{30}°}\\{\mathrm{sin}\:\mathrm{30}°}\end{pmatrix}={f}_{\mathrm{1}} \begin{pmatrix}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix} \\ $$$${F}_{\mathrm{2}} ={f}_{\mathrm{2}} \begin{pmatrix}{\mathrm{cos}\:\mathrm{120}°}\\{\mathrm{sin}\:\mathrm{120}°}\end{pmatrix}={f}_{\mathrm{2}} \begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{pmatrix} \\ $$$${F}_{\mathrm{3}} ={f}_{\mathrm{3}} \begin{pmatrix}{\mathrm{cos}\:\mathrm{210}°}\\{\mathrm{sin}\:\mathrm{210}°}\end{pmatrix}={f}_{\mathrm{3}} \begin{pmatrix}{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{−\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix} \\ $$$${F}_{\mathrm{1}} +{F}_{\mathrm{2}} +{F}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\sqrt{\mathrm{3}}{f}_{\mathrm{1}} −{f}_{\mathrm{2}} −\sqrt{\mathrm{3}}{f}_{\mathrm{3}} }\\{{f}_{\mathrm{1}} +\sqrt{\mathrm{3}}{f}_{\mathrm{2}} −{f}_{\mathrm{3}} }\end{pmatrix}= \\ $$$$\:\:\:\:\:\left[\mathrm{if}\:{f}_{\mathrm{1}} ={f}_{\mathrm{2}} ={f}_{\mathrm{3}} ={f}\right] \\ $$$$=\frac{{f}}{\mathrm{2}}\begin{pmatrix}{\mathrm{1}}\\{\sqrt{\mathrm{3}}}\end{pmatrix} \\ $$
