Menu Close

Three-tennis-players-A-B-and-C-play-each-other-only-once-The-probability-that-A-will-beat-B-is-3-5-that-B-will-beat-C-is-2-3-and-that-A-will-beat-C-is-5-7-Find-1-the-probability-that-A-wi

Tinku Tara 0 Comments
Pin




Question Number 19393 by myintkhaing last updated on 10/Aug/17
Three tennis players A, B and C play each other only once. The probability that A will beat B is (3/5), that B will beat C is (2/3), and that A will beat C is (5/7). Find (1) the probability that A will not win both games (2) the probability that A will win not both games.
$$\mathrm{Three}\:\mathrm{tennis}\:\mathrm{players}\:\mathrm{A},\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{play}\:\mathrm{each} \\ $$$$\mathrm{other}\:\mathrm{only}\:\mathrm{once}.\:\mathrm{The}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{A}\:\mathrm{will} \\ $$$$\mathrm{beat}\:\mathrm{B}\:\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{5}},\:\mathrm{that}\:\mathrm{B}\:\mathrm{will}\:\mathrm{beat}\:\mathrm{C}\:\mathrm{is}\:\frac{\mathrm{2}}{\mathrm{3}},\:\mathrm{and}\:\mathrm{that} \\ $$$$\mathrm{A}\:\mathrm{will}\:\mathrm{beat}\:\mathrm{C}\:\mathrm{is}\:\frac{\mathrm{5}}{\mathrm{7}}.\:\mathrm{Find}\:\left(\mathrm{1}\right)\:\mathrm{the}\:\mathrm{probability} \\ $$$$\mathrm{that}\:\mathrm{A}\:\mathrm{will}\:\mathrm{not}\:\mathrm{win}\:\mathrm{both}\:\mathrm{games} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{A}\:\mathrm{will}\:\mathrm{win}\:\mathrm{not}\:\mathrm{both}\:\mathrm{games}. \\ $$
Answered by allizzwell23 last updated on 10/Aug/17
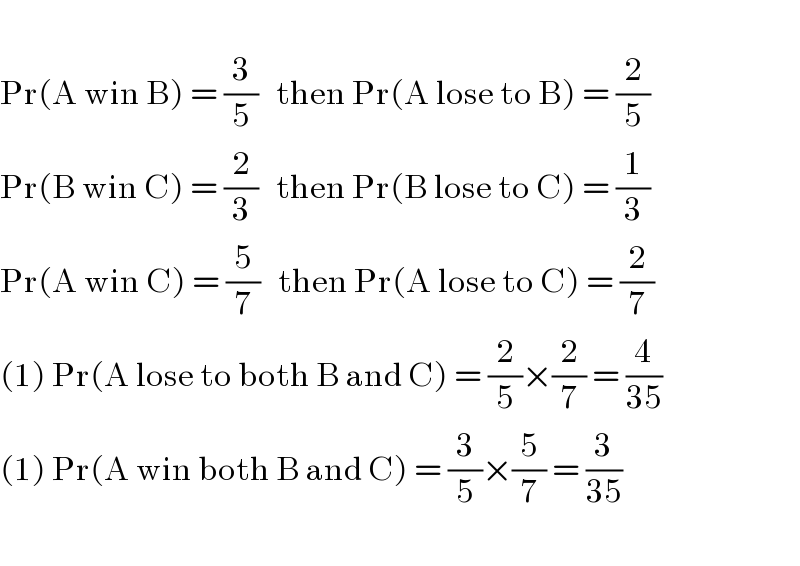
Pr(A win B) = (3/5) then Pr(A lose to B) = (2/5) Pr(B win C) = (2/3) then Pr(B lose to C) = (1/3) Pr(A win C) = (5/7) then Pr(A lose to C) = (2/7) (1) Pr(A lose to both B and C) = (2/5)×(2/7) = (4/(35)) (1) Pr(A win both B and C) = (3/5)×(5/7) = (3/(35))
$$ \\ $$$$\mathrm{Pr}\left(\mathrm{A}\:\mathrm{win}\:\mathrm{B}\right)\:=\:\frac{\mathrm{3}}{\mathrm{5}}\:\:\:\mathrm{then}\:\mathrm{Pr}\left(\mathrm{A}\:\mathrm{lose}\:\mathrm{to}\:\mathrm{B}\right)\:=\:\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\mathrm{Pr}\left(\mathrm{B}\:\mathrm{win}\:\mathrm{C}\right)\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\mathrm{then}\:\mathrm{Pr}\left(\mathrm{B}\:\mathrm{lose}\:\mathrm{to}\:\mathrm{C}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{Pr}\left(\mathrm{A}\:\mathrm{win}\:\mathrm{C}\right)\:=\:\frac{\mathrm{5}}{\mathrm{7}}\:\:\:\mathrm{then}\:\mathrm{Pr}\left(\mathrm{A}\:\mathrm{lose}\:\mathrm{to}\:\mathrm{C}\right)\:=\:\frac{\mathrm{2}}{\mathrm{7}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Pr}\left(\mathrm{A}\:\mathrm{lose}\:\mathrm{to}\:\mathrm{both}\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\right)\:=\:\frac{\mathrm{2}}{\mathrm{5}}×\frac{\mathrm{2}}{\mathrm{7}}\:=\:\frac{\mathrm{4}}{\mathrm{35}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Pr}\left(\mathrm{A}\:\mathrm{win}\:\mathrm{both}\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\right)\:=\:\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{5}}{\mathrm{7}}\:=\:\frac{\mathrm{3}}{\mathrm{35}} \\ $$$$ \\ $$
Commented by myintkhaing last updated on 11/Aug/17
please check No.(2) Tinkutara
$$\mathrm{please}\:\mathrm{check}\:\mathrm{No}.\left(\mathrm{2}\right)\:\mathrm{Tinkutara} \\ $$
Commented by Tinkutara last updated on 11/Aug/17
Yes your solution is true. Sorry for my mistake.
$$\mathrm{Yes}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{true}.\:\mathrm{Sorry}\:\mathrm{for}\:\mathrm{my} \\ $$$$\mathrm{mistake}. \\ $$
Commented by myintkhaing last updated on 11/Aug/17
Let > means beat. (A>B means A will beat B) A>B ∣ A<B B>C ∣ B<C ∣ B>C ∣ B<C A>C∣A<C∣A>C∣A<C∣A>C∣A<C∣A>C∣A<C (i) (ii) (iii) (iv) (v) (vi) (vii) (viii) number of all possible outcomes = 8 For A will win both games, we choose event (i) and (iii) So, P(A will win both games)=(3/5)×(2/3)×(5/7)+(3/5)×(1/3)×(5/7)=(3/7) ∴ P(A will not win both games)=1−P(A will win both games) =(4/7) (OR) P(A will win not both games)=1−P(A will win both games) =(4/7) Which solution is true? Please.
$$\mathrm{Let}\:>\:\mathrm{means}\:\mathrm{beat}.\:\left(\mathrm{A}>\mathrm{B}\:\mathrm{means}\:\mathrm{A}\:\mathrm{will}\:\mathrm{beat}\:\mathrm{B}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{A}>\mathrm{B}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{A}<\mathrm{B} \\ $$$$\:\:\:\:\:\:\:\mathrm{B}>\mathrm{C}\:\:\:\:\:\:\:\mid\:\:\:\:\:\:\:\mathrm{B}<\mathrm{C}\:\:\:\:\:\:\:\mid\:\:\:\:\:\:\:\:\mathrm{B}>\mathrm{C}\:\:\:\:\:\:\mid\:\:\:\:\:\:\:\mathrm{B}<\mathrm{C} \\ $$$$\mathrm{A}>\mathrm{C}\mid\mathrm{A}<\mathrm{C}\mid\mathrm{A}>\mathrm{C}\mid\mathrm{A}<\mathrm{C}\mid\mathrm{A}>\mathrm{C}\mid\mathrm{A}<\mathrm{C}\mid\mathrm{A}>\mathrm{C}\mid\mathrm{A}<\mathrm{C} \\ $$$$\:\:\:\left(\mathrm{i}\right)\:\:\:\:\:\:\:\left(\mathrm{ii}\right)\:\:\:\:\:\:\left(\mathrm{iii}\right)\:\:\:\:\:\left(\mathrm{iv}\right)\:\:\:\:\:\:\left(\mathrm{v}\right)\:\:\:\:\:\left(\mathrm{vi}\right)\:\:\:\:\left(\mathrm{vii}\right)\:\:\:\left(\mathrm{viii}\right) \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{outcomes}\:=\:\mathrm{8} \\ $$$$\mathrm{For}\:\mathrm{A}\:\mathrm{will}\:\mathrm{win}\:\mathrm{both}\:\mathrm{games},\:\mathrm{we}\:\mathrm{choose}\:\mathrm{event}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{iii}\right) \\ $$$$\mathrm{So},\:\mathrm{P}\left(\mathrm{A}\:\mathrm{will}\:\mathrm{win}\:\mathrm{both}\:\mathrm{games}\right)=\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{5}}{\mathrm{7}}+\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{5}}{\mathrm{7}}=\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\therefore\:\mathrm{P}\left(\mathrm{A}\:\mathrm{will}\:\mathrm{not}\:\mathrm{win}\:\mathrm{both}\:\mathrm{games}\right)=\mathrm{1}−\mathrm{P}\left(\mathrm{A}\:\mathrm{will}\:\mathrm{win}\:\mathrm{both}\:\mathrm{games}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}}{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{OR}\right) \\ $$$$\mathrm{P}\left(\mathrm{A}\:\mathrm{will}\:\mathrm{win}\:\mathrm{not}\:\mathrm{both}\:\mathrm{games}\right)=\mathrm{1}−\mathrm{P}\left(\mathrm{A}\:\mathrm{will}\:\mathrm{win}\:\mathrm{both}\:\mathrm{games}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}}{\mathrm{7}} \\ $$$$\mathrm{Which}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{true}?\:\mathrm{Please}. \\ $$
Commented by myintkhaing last updated on 12/Aug/17
Thank you. Are you used facebook, Tinkutara?
$$\mathrm{Thank}\:\mathrm{you}.\:\mathrm{Are}\:\mathrm{you}\:\mathrm{used}\:\mathrm{facebook},\:\mathrm{Tinkutara}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *