Question Number 26328 by tawa tawa last updated on 24/Dec/17

$$\mathrm{Three}\:\mathrm{towns}\:\mathrm{X},\:\mathrm{Y}\:\mathrm{and}\:\mathrm{Z}\:\mathrm{are}\:\mathrm{on}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{road}\:\mathrm{and}\:\mathrm{Y}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mid}−\mathrm{way}\:\mathrm{between} \\ $$$$\mathrm{X}\:\mathrm{and}\:\mathrm{Z}.\:\mathrm{A}\:\mathrm{motor}\:\mathrm{cyclist}\:\mathrm{moving}\:\mathrm{with}\:\mathrm{uniform}\:\mathrm{acceleration}\:\mathrm{passes}\:\mathrm{X},\:\mathrm{Y}\:\mathrm{and}\:\mathrm{Z}.\: \\ $$$$\mathrm{The}\:\mathrm{speed}\:\mathrm{with}\:\mathrm{which}\:\mathrm{the}\:\mathrm{motocyclist}\:\mathrm{passes}\:\mathrm{X}\:\mathrm{and}\:\mathrm{Z}\:\mathrm{are}\:\mathrm{20m}/\mathrm{s}\:\mathrm{and}\:\mathrm{40m}/\mathrm{s}\: \\ $$$$\mathrm{respectively}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{with}\:\mathrm{which}\:\mathrm{the}\:\mathrm{motorcyclist}\:\mathrm{passes}\:\mathrm{Y}. \\ $$
Commented by tawa tawa last updated on 24/Dec/17

$$\mathrm{please}\:\mathrm{help}. \\ $$
Answered by jota@ last updated on 25/Dec/17
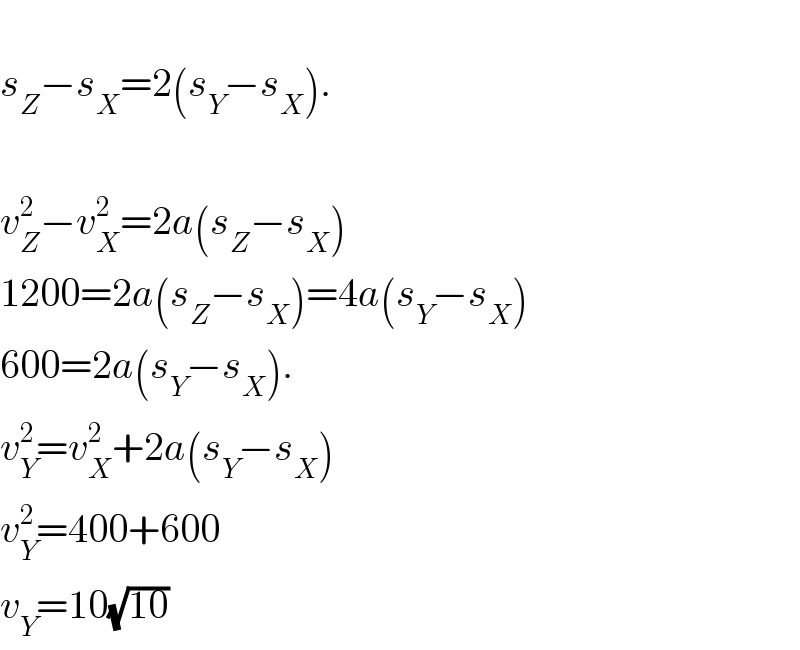
$$ \\ $$$${s}_{{Z}} −{s}_{{X}} =\mathrm{2}\left({s}_{{Y}} −{s}_{{X}} \right). \\ $$$$ \\ $$$${v}_{{Z}} ^{\mathrm{2}} −{v}_{{X}} ^{\mathrm{2}} =\mathrm{2}{a}\left({s}_{{Z}} −{s}_{{X}} \right) \\ $$$$\mathrm{1200}=\mathrm{2}{a}\left({s}_{{Z}} −{s}_{{X}} \right)=\mathrm{4}{a}\left({s}_{{Y}} −{s}_{{X}} \right) \\ $$$$\mathrm{600}=\mathrm{2}{a}\left({s}_{{Y}} −{s}_{{X}} \right). \\ $$$${v}_{{Y}} ^{\mathrm{2}} ={v}_{{X}} ^{\mathrm{2}} +\mathrm{2}{a}\left({s}_{{Y}} −{s}_{{X}} \right) \\ $$$${v}_{{Y}} ^{\mathrm{2}} =\mathrm{400}+\mathrm{600} \\ $$$${v}_{{Y}} =\mathrm{10}\sqrt{\mathrm{10}} \\ $$
Commented by tawa tawa last updated on 25/Dec/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$
