Question Number 104046 by mathocean1 last updated on 19/Jul/20

$$\mathrm{To}\:\mathrm{do}\:\mathrm{normally}\:\mathrm{his}\:\mathrm{commercial} \\ $$$$\mathrm{activities}\:\mathrm{in}\:\mathrm{some}\:\mathrm{place}\:\mathrm{situated}\:\mathrm{at}\:\mathrm{150km} \\ $$$$\mathrm{from}\:\mathrm{him},\:\mathrm{a}\:\mathrm{driver}\:\mathrm{use}\:\mathrm{a}\:\mathrm{car}.\:\mathrm{the}\:\mathrm{consumption} \\ $$$$\mathrm{of}\:\mathrm{gazoil}\:\mathrm{in}\:\mathrm{liters}\:\mathrm{for}\:\mathrm{10}\:\mathrm{km}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{by}: \\ $$$$\mathrm{C}\left(\mathrm{v}\right)=\frac{\mathrm{20}}{\mathrm{v}}+\frac{\mathrm{v}}{\mathrm{45}}\:\mathrm{where}\:\mathrm{v}\:\mathrm{is}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{car}. \\ $$$$\mathrm{How}\:\mathrm{should}\:\mathrm{be}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{car}\:\mathrm{to}\:\mathrm{reduce} \\ $$$$\mathrm{minimally}\:\mathrm{the}\:\mathrm{consumption}\:\mathrm{of}\:\mathrm{gazoil}? \\ $$
Commented by mr W last updated on 19/Jul/20
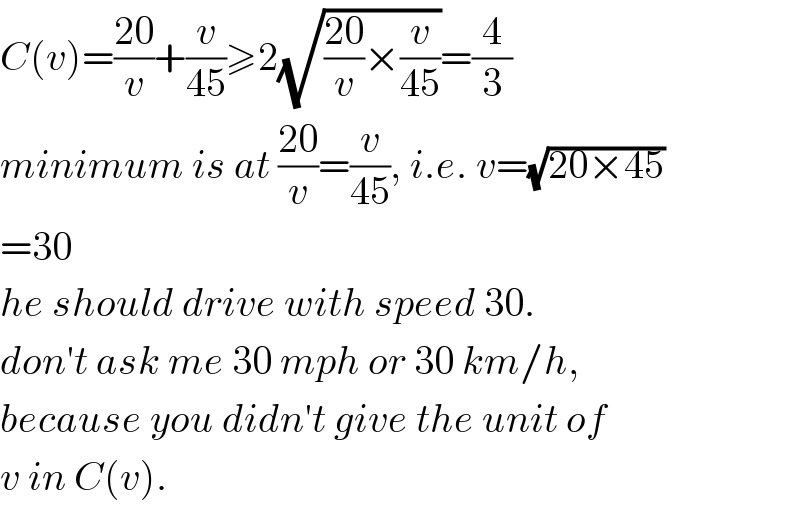
$${C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}}\geqslant\mathrm{2}\sqrt{\frac{\mathrm{20}}{{v}}×\frac{{v}}{\mathrm{45}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${minimum}\:{is}\:{at}\:\frac{\mathrm{20}}{{v}}=\frac{{v}}{\mathrm{45}},\:{i}.{e}.\:{v}=\sqrt{\mathrm{20}×\mathrm{45}} \\ $$$$=\mathrm{30} \\ $$$${he}\:{should}\:{drive}\:{with}\:{speed}\:\mathrm{30}. \\ $$$${don}'{t}\:{ask}\:{me}\:\mathrm{30}\:{mph}\:{or}\:\mathrm{30}\:{km}/{h}, \\ $$$${because}\:{you}\:{didn}'{t}\:{give}\:{the}\:{unit}\:{of} \\ $$$${v}\:{in}\:{C}\left({v}\right). \\ $$
Commented by mathocean1 last updated on 19/Jul/20
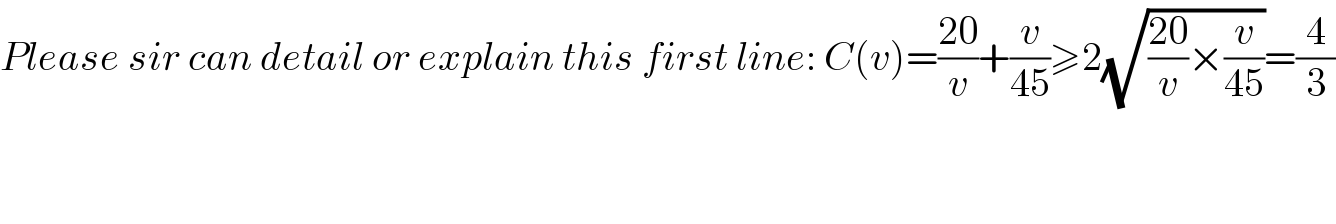
$${Please}\:{sir}\:{can}\:{detail}\:{or}\:{explain}\:{this}\:{first}\:{line}:\:{C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}}\geqslant\mathrm{2}\sqrt{\frac{\mathrm{20}}{{v}}×\frac{{v}}{\mathrm{45}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathocean1 last updated on 19/Jul/20
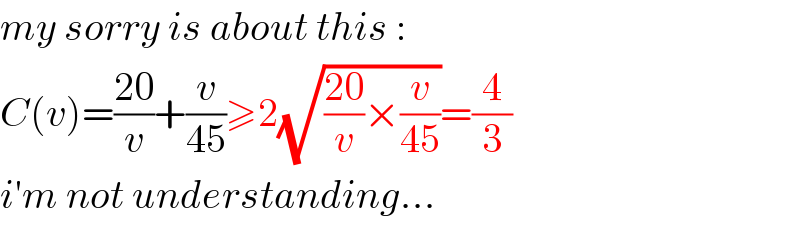
$${my}\:{sorry}\:{is}\:{about}\:{this}\:: \\ $$$${C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}}\geqslant\mathrm{2}\sqrt{\frac{\mathrm{20}}{{v}}×\frac{{v}}{\mathrm{45}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${i}'{m}\:{not}\:{understanding}… \\ $$
Commented by mr W last updated on 19/Jul/20
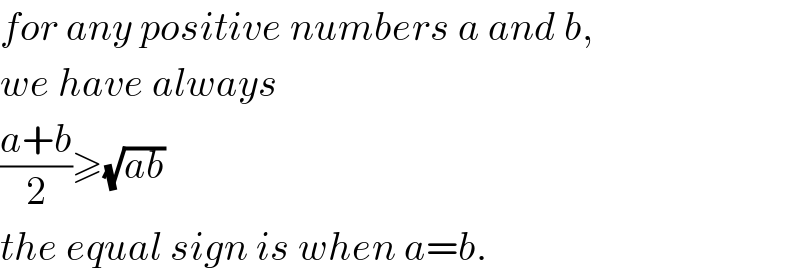
$${for}\:{any}\:{positive}\:{numbers}\:{a}\:{and}\:{b}, \\ $$$${we}\:{have}\:{always} \\ $$$$\frac{{a}+{b}}{\mathrm{2}}\geqslant\sqrt{{ab}} \\ $$$${the}\:{equal}\:{sign}\:{is}\:{when}\:{a}={b}. \\ $$
Commented by mr W last updated on 19/Jul/20
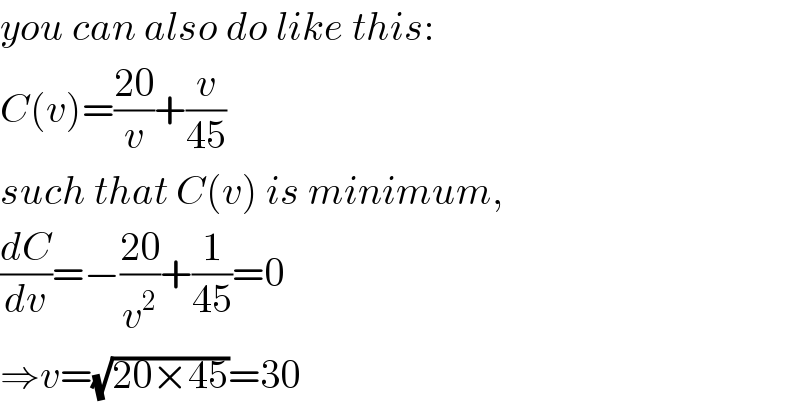
$${you}\:{can}\:{also}\:{do}\:{like}\:{this}: \\ $$$${C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}} \\ $$$${such}\:{that}\:{C}\left({v}\right)\:{is}\:{minimum}, \\ $$$$\frac{{dC}}{{dv}}=−\frac{\mathrm{20}}{{v}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{45}}=\mathrm{0} \\ $$$$\Rightarrow{v}=\sqrt{\mathrm{20}×\mathrm{45}}=\mathrm{30} \\ $$
Commented by mathocean1 last updated on 19/Jul/20
$${thank}\:{you}\:{very}\:{much}\:{sir}! \\ $$
