Question Number 123866 by benjo_mathlover last updated on 28/Nov/20
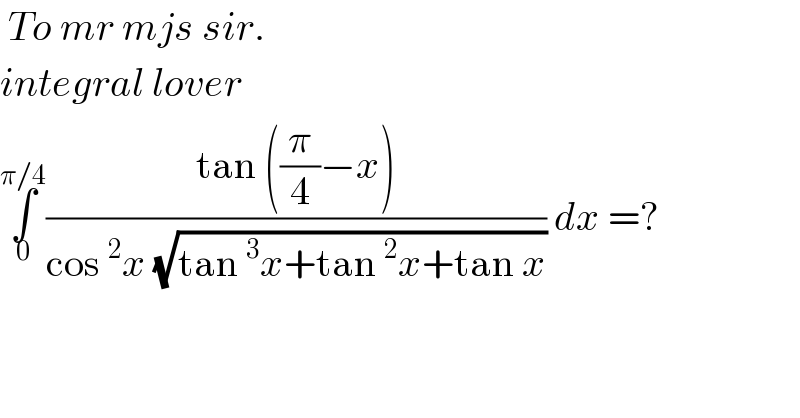
$$\:{To}\:{mr}\:{mjs}\:{sir}.\: \\ $$$${integral}\:{lover}\: \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)}{\mathrm{cos}\:^{\mathrm{2}} {x}\:\sqrt{\mathrm{tan}\:^{\mathrm{3}} {x}+\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{tan}\:{x}}}\:{dx}\:=?\: \\ $$
Answered by liberty last updated on 28/Nov/20
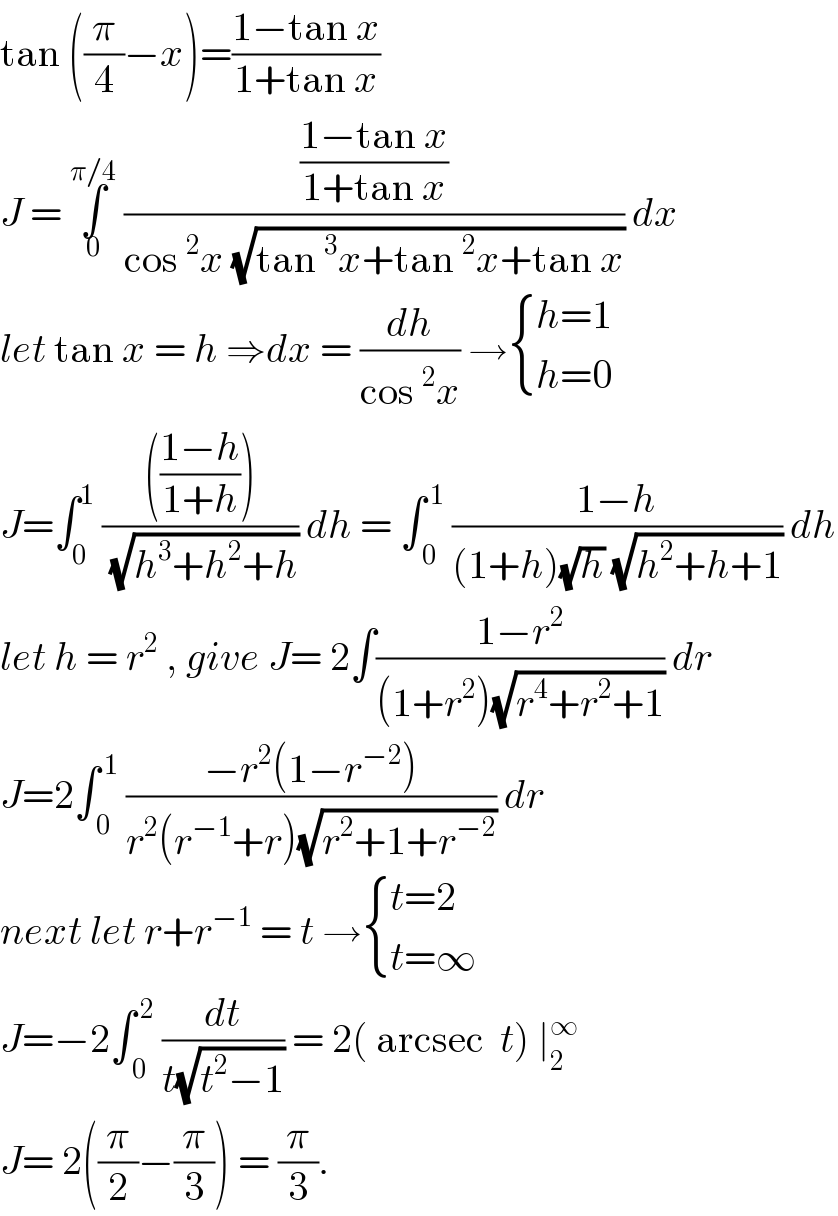
$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)=\frac{\mathrm{1}−\mathrm{tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:{x}} \\ $$$${J}\:=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\frac{\mathrm{1}−\mathrm{tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:{x}}}{\mathrm{cos}\:^{\mathrm{2}} {x}\:\sqrt{\mathrm{tan}\:^{\mathrm{3}} {x}+\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{tan}\:{x}}}\:{dx} \\ $$$${let}\:\mathrm{tan}\:{x}\:=\:{h}\:\Rightarrow{dx}\:=\:\frac{{dh}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:\rightarrow\begin{cases}{{h}=\mathrm{1}}\\{{h}=\mathrm{0}}\end{cases} \\ $$$${J}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\frac{\mathrm{1}−{h}}{\mathrm{1}+{h}}\right)}{\:\sqrt{{h}^{\mathrm{3}} +{h}^{\mathrm{2}} +{h}}}\:{dh}\:=\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}−{h}}{\left(\mathrm{1}+{h}\right)\sqrt{{h}}\:\sqrt{{h}^{\mathrm{2}} +{h}+\mathrm{1}}}\:{dh} \\ $$$${let}\:{h}\:=\:{r}^{\mathrm{2}} \:,\:{give}\:{J}=\:\mathrm{2}\int\frac{\mathrm{1}−{r}^{\mathrm{2}} }{\left(\mathrm{1}+{r}^{\mathrm{2}} \right)\sqrt{{r}^{\mathrm{4}} +{r}^{\mathrm{2}} +\mathrm{1}}}\:{dr} \\ $$$${J}=\mathrm{2}\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\frac{−{r}^{\mathrm{2}} \left(\mathrm{1}−{r}^{−\mathrm{2}} \right)}{{r}^{\mathrm{2}} \left({r}^{−\mathrm{1}} +{r}\right)\sqrt{{r}^{\mathrm{2}} +\mathrm{1}+{r}^{−\mathrm{2}} }}\:{dr}\: \\ $$$${next}\:{let}\:{r}+{r}^{−\mathrm{1}} \:=\:{t}\:\rightarrow\begin{cases}{{t}=\mathrm{2}}\\{{t}=\infty}\end{cases} \\ $$$${J}=−\mathrm{2}\int_{\:\mathrm{0}} ^{\:\mathrm{2}} \:\frac{{dt}}{{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\:=\:\mathrm{2}\left(\:\mathrm{arcsec}\:\:{t}\right)\:\mid_{\mathrm{2}} ^{\infty} \\ $$$${J}=\:\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\right)\:=\:\frac{\pi}{\mathrm{3}}. \\ $$
Answered by MJS_new last updated on 29/Nov/20
![tan ((π/4)−x) =((1−tan x)/(1+tan x)) cos^2 x =(1/(1+tan^2 x)) let me write τ for tan x now we have −∫_0 ^(π/4) (((τ−1)(τ^2 +1))/((τ+1)(√(τ(τ^2 +τ+1)))))dx= =[t=((√τ)/( (√(τ^2 +τ+1)))) → dx=−((2(τ^2 +τ+1)^(3/2) (√τ))/((τ^2 −1)(τ^2 +1)))dt] =2∫_0 ^((√3)/3) ((τ^2 +τ+1)/((τ^2 +1)^2 ))dt= [τ=tan x =−((t^2 −1−(√(−3t^4 −2t^2 +1)))/(2t^2 ))] =2∫_0 ^((√3)/3) (dt/(t^2 +1))=2arctan t =(π/3) [2arctan t =arccos ((1−t^2 )/(1+t^2 )) =arccos (1/(1+sin 2x))]](https://www.tinkutara.com/question/Q123941.png)
$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)\:=\frac{\mathrm{1}−\mathrm{tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:{x}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}} \\ $$$$\mathrm{let}\:\mathrm{me}\:\mathrm{write}\:\tau\:\mathrm{for}\:\mathrm{tan}\:{x} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$−\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{\left(\tau−\mathrm{1}\right)\left(\tau^{\mathrm{2}} +\mathrm{1}\right)}{\left(\tau+\mathrm{1}\right)\sqrt{\tau\left(\tau^{\mathrm{2}} +\tau+\mathrm{1}\right)}}{dx}= \\ $$$$=\left[{t}=\frac{\sqrt{\tau}}{\:\sqrt{\tau^{\mathrm{2}} +\tau+\mathrm{1}}}\:\rightarrow\:{dx}=−\frac{\mathrm{2}\left(\tau^{\mathrm{2}} +\tau+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \sqrt{\tau}}{\left(\tau^{\mathrm{2}} −\mathrm{1}\right)\left(\tau^{\mathrm{2}} +\mathrm{1}\right)}{dt}\right] \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{3}}/\mathrm{3}} {\int}}\:\frac{\tau^{\mathrm{2}} +\tau+\mathrm{1}}{\left(\tau^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\tau=\mathrm{tan}\:{x}\:=−\frac{{t}^{\mathrm{2}} −\mathrm{1}−\sqrt{−\mathrm{3}{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}{t}^{\mathrm{2}} }\right] \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{3}}/\mathrm{3}} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2arctan}\:{t}\:=\frac{\pi}{\mathrm{3}} \\ $$$$\left[\mathrm{2arctan}\:{t}\:=\mathrm{arccos}\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{arccos}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}}\right] \\ $$
