To-the-member-in-forum-please-give-an-opinion-on-this-matter-George-Lucia-and-12-of-their-friends-will-sit-around-a-round-table-Many-of-their-arrangements-sit-if-George-and-Lucia-always-flank-5

Question Number 82975 by jagoll last updated on 26/Feb/20

$$\mathrm{To}\:\mathrm{the}\:\mathrm{member}\:\mathrm{in}\:\mathrm{forum}.\:\mathrm{please}\: \\ $$$$\mathrm{give}\:\mathrm{an}\:\mathrm{opinion}\:\mathrm{on}\:\mathrm{this}\:\mathrm{matter}. \\ $$$$\mathrm{George}\:,\:\mathrm{Lucia}\:\mathrm{and}\:\mathrm{12}\:\mathrm{of}\:\mathrm{their} \\ $$$$\mathrm{friends}\:\mathrm{will}\:\mathrm{sit}\:\mathrm{around}\:\mathrm{a}\:\mathrm{round}\:\mathrm{table}. \\ $$$$\mathrm{Many}\:\mathrm{of}\:\mathrm{their}\:\mathrm{arrangements}\:\mathrm{sit}\: \\ $$$$\mathrm{if}\:\mathrm{George}\:\mathrm{and}\:\mathrm{Lucia}\:\mathrm{always}\:\mathrm{flank} \\ $$$$\mathrm{5}\:\mathrm{of}\:\mathrm{their}\:\mathrm{friends}? \\ $$

Commented by jagoll last updated on 26/Feb/20

my answer is 2! C_5 ^( 12) 5! 7! it correct?

$$\mathrm{my}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2}!\:\mathrm{C}_{\mathrm{5}} ^{\:\mathrm{12}} \:\mathrm{5}!\:\mathrm{7}!\: \\ $$$$\mathrm{it}\:\mathrm{correct}? \\ $$

Commented by mr W last updated on 26/Feb/20

let′s fix the sit of Geoge. to place the sit of Lucia there are two ways. to arrange the 12 friends there are 12! ways, therefore the answer is 2×12!.

$${let}'{s}\:{fix}\:{the}\:{sit}\:{of}\:{Geoge}.\:{to}\:{place}\:{the} \\ $$$${sit}\:{of}\:{Lucia}\:{there}\:{are}\:{two}\:{ways}.\:{to} \\ $$$${arrange}\:{the}\:\mathrm{12}\:{friends}\:{there}\:{are}\:\mathrm{12}! \\ $$$${ways},\:{therefore}\:{the}\:{answer}\:{is}\:\mathrm{2}×\mathrm{12}!. \\ $$

Commented by john santu last updated on 26/Feb/20

in my opinion the answer is correct 2! C_5 ^(12) 5!7!

$$\mathrm{in}\:\mathrm{my}\:\mathrm{opinion}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct} \\ $$$$\mathrm{2}!\:\mathrm{C}_{\mathrm{5}} ^{\mathrm{12}} \mathrm{5}!\mathrm{7}!\: \\ $$

Commented by jagoll last updated on 26/Feb/20

$$\mathrm{why}\:\mathrm{sir}?\: \\ $$

Commented by jagoll last updated on 26/Feb/20

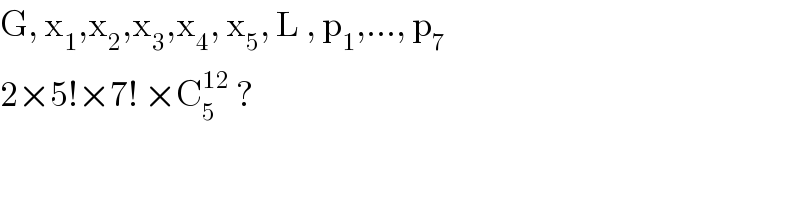
G, x_1 ,x_2 ,x_3 ,x_4 , x_5 , L , p_1 ,..., p_(7 ) 2×5!×7! ×C_5 ^(12) ?

Commented by mr W last updated on 26/Feb/20

G, x_1 ,x_2 ,x_3 ,x_4 , x_5 , L , x_6 ,..., x_(12) L, x_1 ,x_2 ,x_3 ,x_4 , x_5 , G , x_6 ,..., x_(12) ⇒2×12! numerically 2×5!×7! ×C_5 ^(12) =2×12!, but i think we don′t need to think too complicated.

$$\mathrm{G},\:\mathrm{x}_{\mathrm{1}} ,\mathrm{x}_{\mathrm{2}} ,\mathrm{x}_{\mathrm{3}} ,\mathrm{x}_{\mathrm{4}} ,\:\mathrm{x}_{\mathrm{5}} ,\:\mathrm{L}\:,\:{x}_{\mathrm{6}} ,…,\:{x}_{\mathrm{12}} \\ $$$${L},\:\mathrm{x}_{\mathrm{1}} ,\mathrm{x}_{\mathrm{2}} ,\mathrm{x}_{\mathrm{3}} ,\mathrm{x}_{\mathrm{4}} ,\:\mathrm{x}_{\mathrm{5}} ,\:{G}\:,\:{x}_{\mathrm{6}} ,…,\:{x}_{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{2}×\mathrm{12}! \\ $$$${numerically}\:\mathrm{2}×\mathrm{5}!×\mathrm{7}!\:×\mathrm{C}_{\mathrm{5}} ^{\mathrm{12}} =\mathrm{2}×\mathrm{12}!, \\ $$$${but}\:{i}\:{think}\:{we}\:{don}'{t}\:{need}\:{to}\:{think}\:{too} \\ $$$${complicated}. \\ $$

Commented by jagoll last updated on 26/Feb/20

hahaha..yes sir. but in option nothing 2×12! . thank you sir. that mean my answer is correct

$$\mathrm{hahaha}..\mathrm{yes}\:\mathrm{sir}.\:\mathrm{but}\:\mathrm{in}\:\mathrm{option}\:\mathrm{nothing} \\ $$$$\mathrm{2}×\mathrm{12}!\:.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{that}\:\mathrm{mean}\:\mathrm{my} \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{correct} \\ $$

Facebook Tweet Pin

To-the-member-in-forum-please-give-an-opinion-on-this-matter-George-Lucia-and-12-of-their-friends-will-sit-around-a-round-table-Many-of-their-arrangements-sit-if-George-and-Lucia-always-flank-5

Leave a Reply Cancel reply