Menu Close

Total-sum-of-this-below-infinite-series-1-1-1-2-1-2-3-1-3-4-1-n-n-1-2-0-6-0-06-0-006-6-10-n-

Tinku Tara 0 Comments
Pin




Question Number 91796 by zainal tanjung last updated on 03/May/20
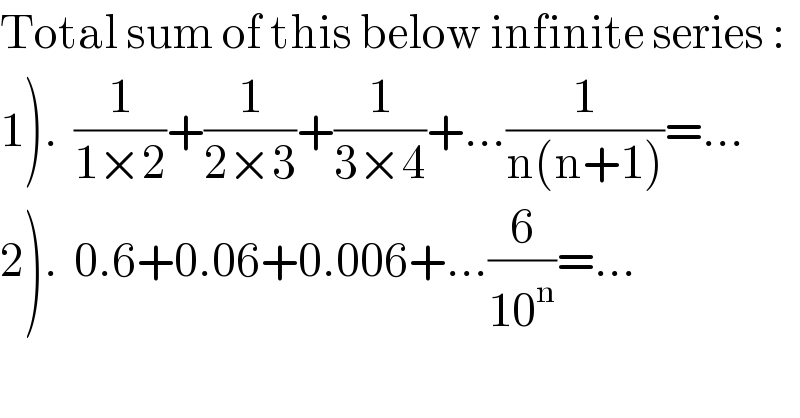
Total sum of this below infinite series : 1). (1/(1×2))+(1/(2×3))+(1/(3×4))+...(1/(n(n+1)))=... 2). 0.6+0.06+0.006+...(6/(10^n ))=...
$$\mathrm{Total}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{this}\:\mathrm{below}\:\mathrm{infinite}\:\mathrm{series}\:: \\ $$$$\left.\mathrm{1}\right).\:\:\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}+…\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}=… \\ $$$$\left.\mathrm{2}\right).\:\:\mathrm{0}.\mathrm{6}+\mathrm{0}.\mathrm{06}+\mathrm{0}.\mathrm{006}+…\frac{\mathrm{6}}{\mathrm{10}^{\mathrm{n}} }=… \\ $$
Commented by mathmax by abdo last updated on 04/May/20
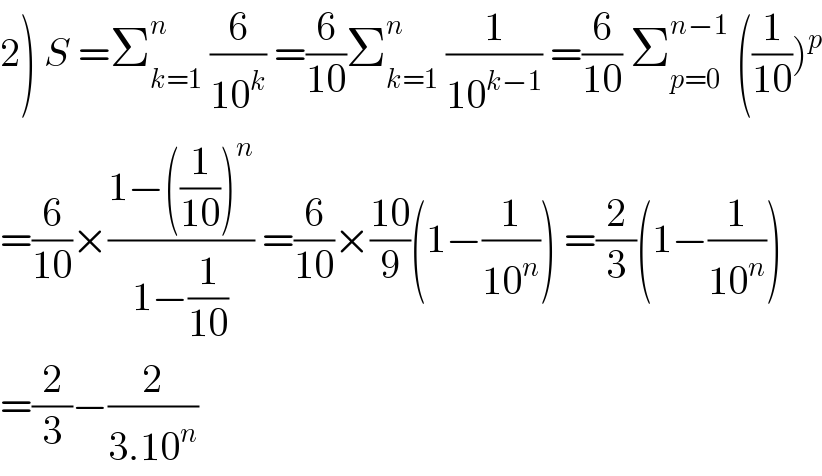
2) S =Σ_(k=1) ^n (6/(10^k )) =(6/(10))Σ_(k=1) ^n (1/(10^(k−1) )) =(6/(10)) Σ_(p=0) ^(n−1) ((1/(10)))^p =(6/(10))×((1−((1/(10)))^n )/(1−(1/(10)))) =(6/(10))×((10)/9)(1−(1/(10^n ))) =(2/3)(1−(1/(10^n ))) =(2/3)−(2/(3.10^n ))
$$\left.\mathrm{2}\right)\:{S}\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{6}}{\mathrm{10}^{{k}} }\:=\frac{\mathrm{6}}{\mathrm{10}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{10}^{{k}−\mathrm{1}} }\:=\frac{\mathrm{6}}{\mathrm{10}}\:\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{10}}\right)^{{p}} \\ $$$$=\frac{\mathrm{6}}{\mathrm{10}}×\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{10}}\right)^{{n}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}}\:=\frac{\mathrm{6}}{\mathrm{10}}×\frac{\mathrm{10}}{\mathrm{9}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}^{{n}} }\right)\:=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}^{{n}} }\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}.\mathrm{10}^{{n}} } \\ $$
Answered by $@ty@m123 last updated on 03/May/20
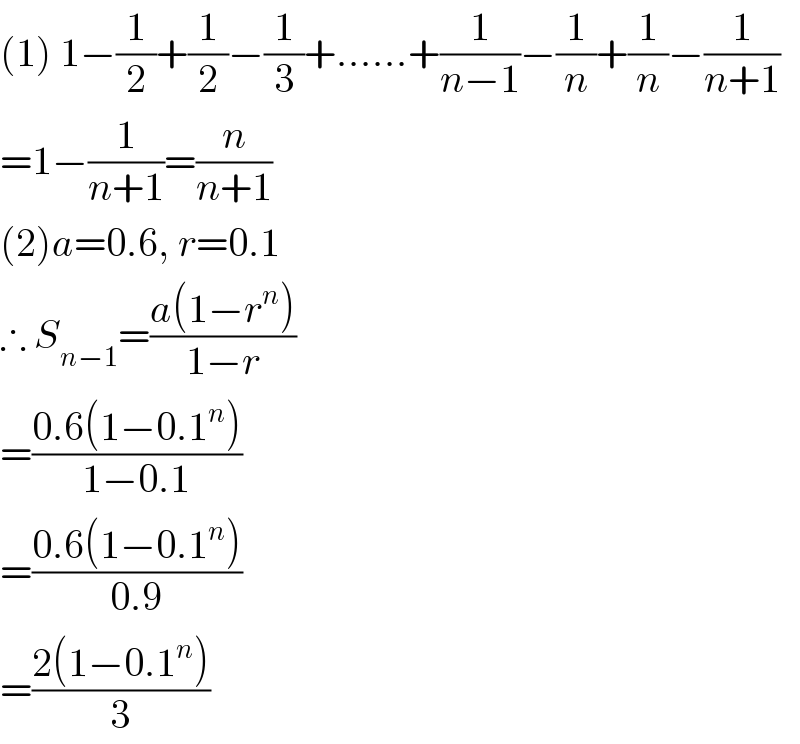
(1) 1−(1/2)+(1/2)−(1/3)+......+(1/(n−1))−(1/n)+(1/n)−(1/(n+1)) =1−(1/(n+1))=(n/(n+1)) (2)a=0.6, r=0.1 ∴ S_(n−1) =((a(1−r^n ))/(1−r)) =((0.6(1−0.1^n ))/(1−0.1)) =((0.6(1−0.1^n ))/(0.9)) =((2(1−0.1^n ))/3)
$$\left(\mathrm{1}\right)\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+……+\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}=\frac{{n}}{{n}+\mathrm{1}} \\ $$$$\left(\mathrm{2}\right){a}=\mathrm{0}.\mathrm{6},\:{r}=\mathrm{0}.\mathrm{1}\: \\ $$$$\therefore\:{S}_{{n}−\mathrm{1}} =\frac{{a}\left(\mathrm{1}−{r}^{{n}} \right)}{\mathrm{1}−{r}} \\ $$$$=\frac{\mathrm{0}.\mathrm{6}\left(\mathrm{1}−\mathrm{0}.\mathrm{1}^{{n}} \right)}{\mathrm{1}−\mathrm{0}.\mathrm{1}} \\ $$$$=\frac{\mathrm{0}.\mathrm{6}\left(\mathrm{1}−\mathrm{0}.\mathrm{1}^{{n}} \right)}{\mathrm{0}.\mathrm{9}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{0}.\mathrm{1}^{{n}} \right)}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *