Question Number 28608 by abdo imad last updated on 27/Jan/18
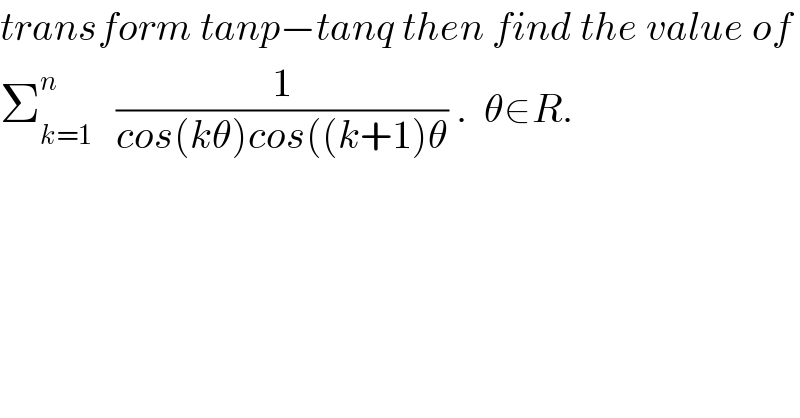
$${transform}\:{tanp}−{tanq}\:{then}\:{find}\:{the}\:{value}\:{of}\: \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{cos}\left({k}\theta\right){cos}\left(\left({k}+\mathrm{1}\right)\theta\right.}\:.\:\:\theta\in{R}. \\ $$
Answered by Tinkutara last updated on 28/Jan/18
![(1/(cos kθcos (k+1)θ)) =((cos [(k+1)θ−kθ])/(cos kθcos (k+1)θcos θ)) =((cos (k+1)θcos θ+sin (k+1)θsin θ)/(cos kθcos (k+1)θcos θ)) =((1+tan (k+1)θtan θ)/(cos θ)) =((tan (k+1)θ−tan θ)/(sin θ)) Telescoping it becomes Σ_(k=1) ^n ((tan (k+1)θ−tan θ)/(sin θ)) =((tan (n+1)θ−tan θ)/(sin θ))](https://www.tinkutara.com/question/Q28630.png)
$$\frac{\mathrm{1}}{\mathrm{cos}\:{k}\theta\mathrm{cos}\:\left({k}+\mathrm{1}\right)\theta} \\ $$$$=\frac{\mathrm{cos}\:\left[\left({k}+\mathrm{1}\right)\theta−{k}\theta\right]}{\mathrm{cos}\:{k}\theta\mathrm{cos}\:\left({k}+\mathrm{1}\right)\theta\mathrm{cos}\:\theta} \\ $$$$=\frac{\mathrm{cos}\:\left({k}+\mathrm{1}\right)\theta\mathrm{cos}\:\theta+\mathrm{sin}\:\left({k}+\mathrm{1}\right)\theta\mathrm{sin}\:\theta}{\mathrm{cos}\:{k}\theta\mathrm{cos}\:\left({k}+\mathrm{1}\right)\theta\mathrm{cos}\:\theta} \\ $$$$=\frac{\mathrm{1}+\mathrm{tan}\:\left({k}+\mathrm{1}\right)\theta\mathrm{tan}\:\theta}{\mathrm{cos}\:\theta} \\ $$$$=\frac{\mathrm{tan}\:\left({k}+\mathrm{1}\right)\theta−\mathrm{tan}\:\theta}{\mathrm{sin}\:\theta} \\ $$$${Telescoping}\:{it}\:{becomes} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{tan}\:\left({k}+\mathrm{1}\right)\theta−\mathrm{tan}\:\theta}{\mathrm{sin}\:\theta} \\ $$$$=\frac{\mathrm{tan}\:\left({n}+\mathrm{1}\right)\theta−\mathrm{tan}\:\theta}{\mathrm{sin}\:\theta} \\ $$
