Question Number 23707 by Tinkutara last updated on 04/Nov/17

Commented by Tinkutara last updated on 04/Nov/17
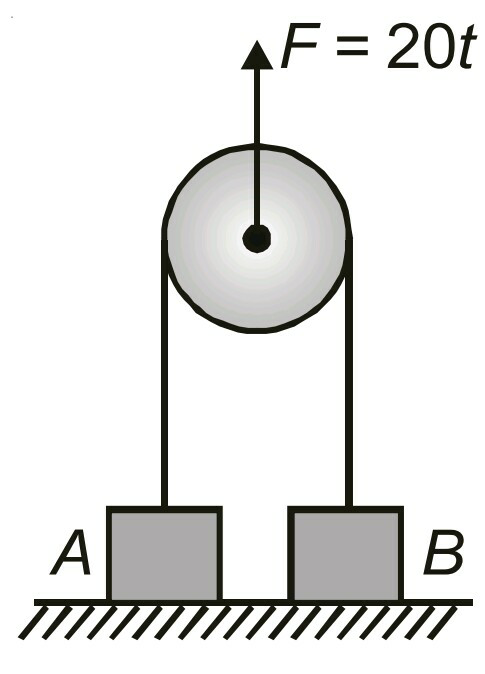
Commented by mrW1 last updated on 05/Nov/17
![I will try. Force in string is T. T=(F/2)=((20t)/2)=10t a_A =((T−m_A g)/m_A )=((10t−m_A g)/m_A )=((10t−10)/1)=10(t−1) a_B =((T−m_B g)/m_B )=((10t−m_B g)/m_B )=((10t−20)/2)=5(t−2) we see when t≥1 mass A is off ground and when t≥2 mass B is off ground. s_P =displacement of pulley v_P =velocity of pulley a_P =acceleration of pulley generally a_P =((a_A +a_B )/2) Phase (1): 0≤t≤1 both blocks are on ground, no motion. a_P =0, v_P =0, s_P =0. Phase (2): 1≤t≤2 block A is off ground with a_A =10(t−1). block B is still on ground a_B =0. a_P =((10(t−1))/2)=5(t−1) ⇒(dv_P /dt)=5(t−1) ∫_0 ^( v_P ) dv_P =5∫_1 ^t (t−1)dt v_P =(5/2)×[(t−1)^2 ]_1 ^t =((5(t−1)^2 )/2) ⇒(ds_P /dt)=((5(t−1)^2 )/2) ∫_0 ^( s_P ) ds_P =(5/2)∫_1 ^( t) (t−1)^2 dt s_P =(5/6)[(t−1)^3 ]_1 ^t =((5(t−1)^3 )/6) at t=2 v_P (2)=(5/2)(2−1)^2 =(5/2) m/s s_P (2)=(5/6)(2−1)^3 =(5/6) m i.e. as the block B takes off from ground the pulley has a displacement of (5/6) m. Phase (3): 2≤t both blocks are off ground. a_P =((10(t−1)+5(t−1))/2)=((15(t−1))/2) (dv_P /dt)=((15)/2)(t−1) ∫_(5/2) ^( v_P ) dv_P =((15)/2)∫_2 ^( t) (t−1)dt v_p −(5/2)=((15)/4)[(t−1)^2 −1] ⇒v_P =(5/4)[3(t−1)^2 −1] (ds_P /dt)=(5/4)[3(t−1)^2 −1] ∫_(6/5) ^s_P ds_P =(5/4)∫_2 ^( t) [3(t−1)^2 −1]dt s_P −(5/6)=(5/4)[(t−1)^3 −1]−(5/4)(t−2) s_P =(5/4)t(t−1)(t−2)+(5/6)](https://www.tinkutara.com/question/Q23729.png)
Commented by mrW1 last updated on 05/Nov/17
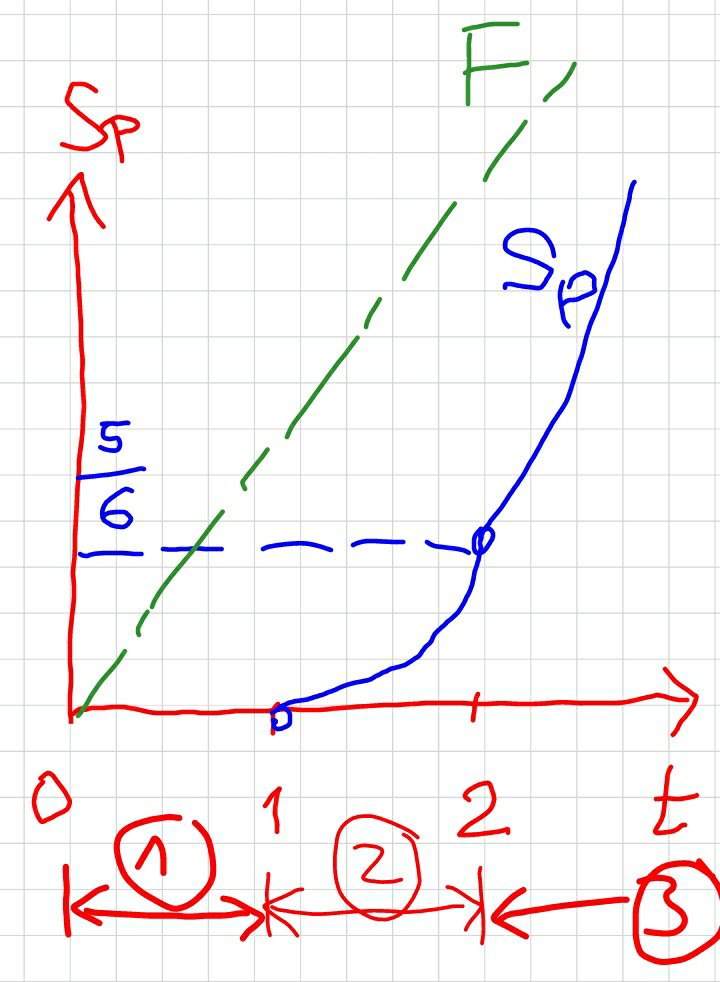
Commented by Tinkutara last updated on 09/Nov/17
Answered by ajfour last updated on 04/Nov/17

Commented by Tinkutara last updated on 04/Nov/17
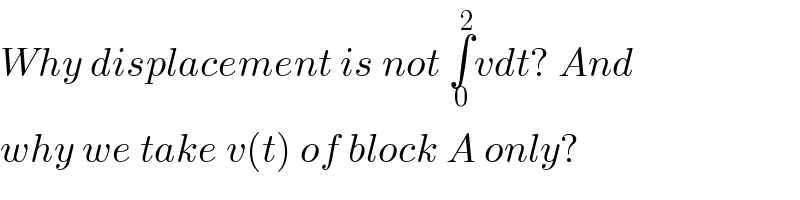
Commented by ajfour last updated on 04/Nov/17
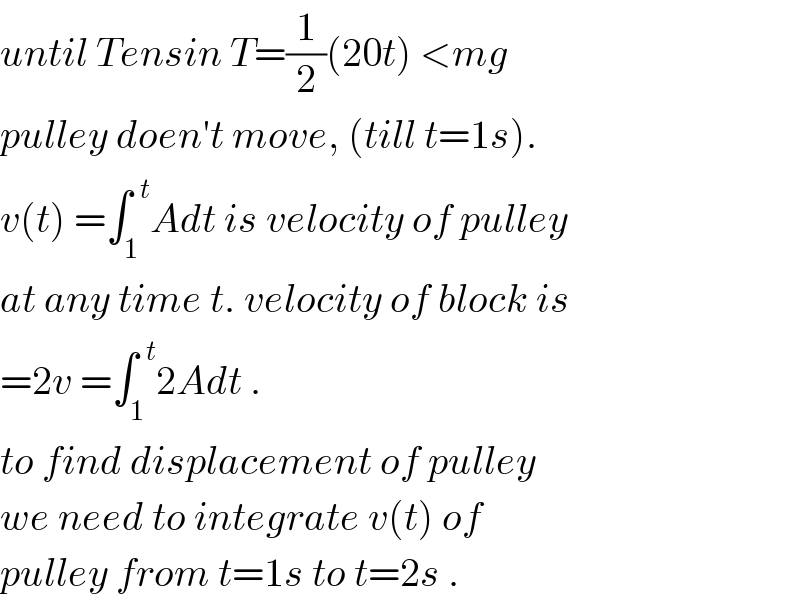
Commented by mrW1 last updated on 09/Nov/17

Commented by Tinkutara last updated on 09/Nov/17
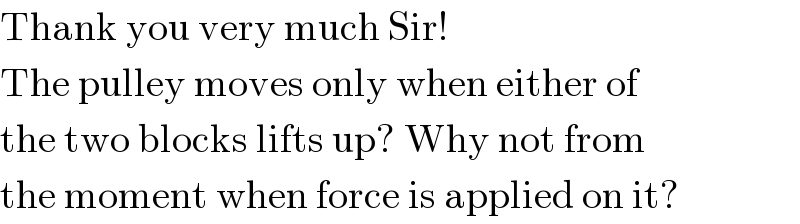
Commented by Tinkutara last updated on 09/Nov/17

Commented by mrW1 last updated on 09/Nov/17

Commented by Tinkutara last updated on 09/Nov/17
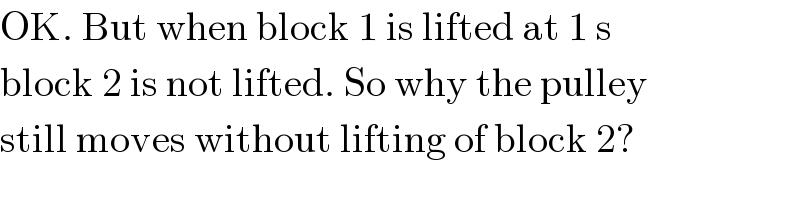
Commented by mrW1 last updated on 09/Nov/17
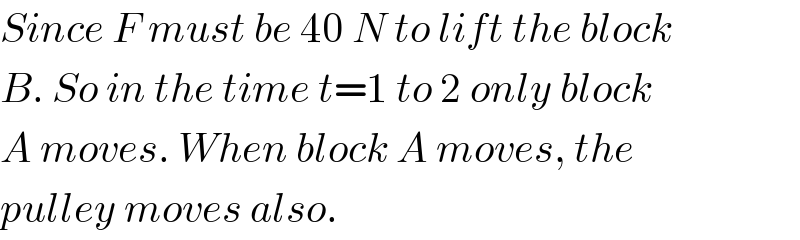
Commented by Tinkutara last updated on 09/Nov/17

