Question Number 113657 by Ar Brandon last updated on 14/Sep/20

$$\mathrm{Two}\:\mathrm{guns}\:\mathrm{situated}\:\mathrm{at}\:\mathrm{the}\:\mathrm{top}\:\mathrm{of}\:\mathrm{a}\:\mathrm{hill}\:\mathrm{of}\:\mathrm{height}\:\mathrm{10m},\:\mathrm{fire}\:\mathrm{one}\:\mathrm{shot}\:\mathrm{each}\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{speed}\:\mathrm{5}\sqrt{\mathrm{3}}\mathrm{ms}^{−\mathrm{1}} \:\mathrm{at}\:\mathrm{some}\:\mathrm{interval}\:\mathrm{of}\:\mathrm{time}.\:\mathrm{One}\:\mathrm{gun}\:\mathrm{fires}\:\mathrm{horizontally} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{other}\:\mathrm{fires}\:\mathrm{upwards}\:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{60}°\:\mathrm{with}\:\mathrm{the}\:\mathrm{horizontal}.\:\mathrm{The}\:\mathrm{shots} \\ $$$$\mathrm{collide}\:\mathrm{in}\:\mathrm{air}\:\mathrm{at}\:\mathrm{a}\:\mathrm{point}\:\mathrm{P}.\:\mathrm{Find}\:\left(\mathrm{i}\right)\:\mathrm{the}\:\mathrm{time}\:\mathrm{interval}\:\mathrm{between}\:\mathrm{the}\:\mathrm{firings}\:\mathrm{and} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{the}\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{the}\:\mathrm{hill}\:\mathrm{right}\:\mathrm{below}\:\mathrm{the}\:\mathrm{muzzle}\:\mathrm{and}\:\mathrm{trajectories}\:\mathrm{in}\:\mathrm{x}-\mathrm{y} \\ $$$$\mathrm{plane}. \\ $$
Commented by Dwaipayan Shikari last updated on 14/Sep/20
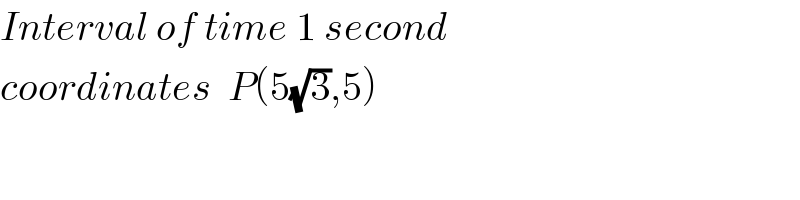
$${Interval}\:{of}\:{time}\:\mathrm{1}\:{second} \\ $$$${coordinates}\:\:{P}\left(\mathrm{5}\sqrt{\mathrm{3}},\mathrm{5}\right) \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 14/Sep/20
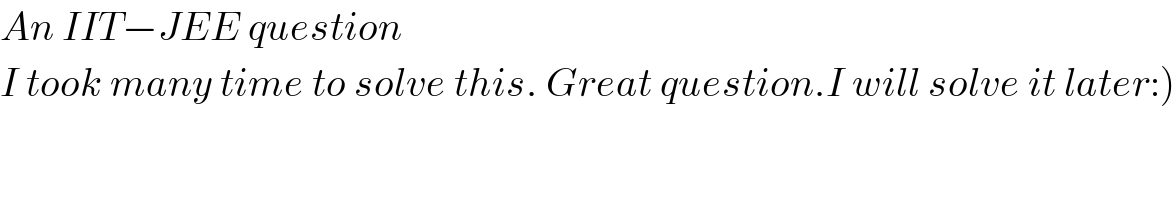
$${An}\:{IIT}−{JEE}\:{question} \\ $$$$\left.{I}\:{took}\:{many}\:{time}\:{to}\:{solve}\:{this}.\:{Great}\:{question}.{I}\:{will}\:{solve}\:{it}\:{later}:\right) \\ $$
Commented by Ar Brandon last updated on 14/Sep/20
Thanks, I found the solution. It's a question from JEE 1996 ��
Commented by Dwaipayan Shikari last updated on 14/Sep/20

$${Particle}\:{A}\:{needs}\:{t}_{\mathrm{1}} \:{time}\:{to}\:{reach}\:{point}\:{P} \\ $$$${Particle}\:{B}\:{t}_{\mathrm{2}} \\ $$$${so}\:\:\:\:\:{upward}\:{velocity}\:=\mathrm{5}\sqrt{\mathrm{3}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:=\frac{\mathrm{15}}{\mathrm{2}}\:\frac{{m}}{{s}}\:\left({At}\:\mathrm{60}°{angle}\right) \\ $$$${After}\:\mathrm{2}\:{seconds}\:\:{its}\:{will}\:{be}\:{at}\:\: \\ $$$${S}=\frac{\mathrm{15}}{\mathrm{2}}.\mathrm{2}−\mathrm{5}\left(\mathrm{4}\right)^{\mathrm{2}} =−\mathrm{5}\:{m}\:\:\:\:\:\left({Relative}\:{height}\right) \\ $$$${After}\:\mathrm{1}\:{second}\:{of}\:{the}\:{first}\:{particle}\:{the}\:{second}\:{particle}\:{starts}\:{flighting} \\ $$$${It}\:{has}\:{no}\:{vertical}\:{velocity}\:\left({free}\:{fall}\right) \\ $$$$\mathrm{1}\:{second}\:{later}\:{It}\:{will}\:{cross}\:{S}=−\frac{\mathrm{1}}{\mathrm{2}}{g}\left(\mathrm{1}\right)^{\mathrm{2}} =−\mathrm{5}{m} \\ $$$${If}\:{they}\:{collide}\:{then}\:{distance}\:{traveled}\:{in}\:{horizontal} \\ $$$$=\left(\mathrm{1}\right).\mathrm{5}\sqrt{\mathrm{3}}\:{m}=\mathrm{5}\sqrt{\mathrm{3}}{m} \\ $$$${So}\:{collision}\:{coordinate}\:{P}\left(\mathrm{5}\sqrt{\mathrm{3}},−\mathrm{5}\right) \\ $$$${And}\:{time}\:{difference}\:=\mathrm{1}{sec} \\ $$
Answered by Ar Brandon last updated on 14/Sep/20

$$\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{Bullet}}\:\boldsymbol{\mathrm{A}}.\:\mathrm{Let}\:\mathrm{t}\:\mathrm{be}\:\mathrm{the}\:\mathrm{time}\:\mathrm{taken}\:\mathrm{by}\:\mathrm{bullet}\:\mathrm{A}\:\mathrm{to}\:\mathrm{reach}\:\mathrm{P}. \\ $$$$\boldsymbol{\mathrm{Verctical}}\:\boldsymbol{\mathrm{motion}} \\ $$$$\mathrm{u}_{\mathrm{y}} =\mathrm{0};\:\mathrm{s}_{\mathrm{y}} =\mathrm{10}−\mathrm{y};\:\mathrm{a}_{\mathrm{y}} =\mathrm{10m}/\mathrm{s}^{\mathrm{2}} ;\:\mathrm{t}_{\mathrm{y}} =\mathrm{t} \\ $$$$\mathrm{s}_{\mathrm{y}} =\mathrm{u}_{\mathrm{y}} \mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}_{\mathrm{y}} \mathrm{t}^{\mathrm{2}} \\ $$$$\mathrm{10}−\mathrm{y}=\mathrm{5t}^{\mathrm{2}} \:\:\:…\left(\mathrm{i}\right) \\ $$$$\boldsymbol{\mathrm{Horizontal}}\:\boldsymbol{\mathrm{motion}} \\ $$$$\mathrm{x}=\mathrm{5}\sqrt{\mathrm{3}}\mathrm{t}\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{bullet}}\:\boldsymbol{\mathrm{B}} \\ $$$$\mathrm{Let}\:\left(\mathrm{t}+\mathrm{t}'\right)\:\mathrm{be}\:\mathrm{the}\:\mathrm{time}\:\mathrm{taken}\:\mathrm{by}\:\mathrm{bullet}\:\mathrm{B}\:\mathrm{to}\:\mathrm{reach}\:\mathrm{P} \\ $$$$\boldsymbol{\mathrm{Vertical}}\:\boldsymbol{\mathrm{Motion}} \\ $$$$\mathrm{Considering}\:\mathrm{updward}\:\mathrm{direction}\:\mathrm{negative} \\ $$$$\mathrm{u}_{\mathrm{y}} =−\mathrm{5}\sqrt{\mathrm{3}}\:\mathrm{sin60}°=−\mathrm{7}.\mathrm{5m}/\mathrm{s},\:\mathrm{a}_{\mathrm{y}} =+\mathrm{10m}/\mathrm{s}^{\mathrm{2}} \\ $$$$\mathrm{s}_{\mathrm{y}} =+\left(\mathrm{10}−\mathrm{y}\right);\:\mathrm{t}_{\mathrm{y}} =\mathrm{t}+\mathrm{t}'\:,\:\mathrm{s}_{\mathrm{y}} =\mathrm{u}_{\mathrm{y}} \mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}_{\mathrm{y}} \mathrm{t}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{10}−\mathrm{y}=−\mathrm{7}.\mathrm{5}\left(\mathrm{t}+\mathrm{t}'\right)+\mathrm{5}\left(\mathrm{t}+\mathrm{t}'\right)^{\mathrm{2}} \:\:…\left(\mathrm{iii}\right) \\ $$$$\boldsymbol{\mathrm{Horizontal}}\:\boldsymbol{\mathrm{motion}} \\ $$$$\mathrm{x}=\left(\mathrm{5}\sqrt{\mathrm{3}}\:\mathrm{cos60}°\right)\left(\mathrm{t}+\mathrm{t}'\right) \\ $$$$\Rightarrow\mathrm{5}\sqrt{\mathrm{3}}\mathrm{t}+\mathrm{5}\sqrt{\mathrm{3}}\:\mathrm{t}'=\mathrm{2x}\:\:…\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{in}\:\left(\mathrm{iv}\right) \\ $$$$\Rightarrow\mathrm{5}\sqrt{\mathrm{3}}\mathrm{t}+\mathrm{5}\sqrt{\mathrm{3}}\mathrm{t}'=\mathrm{10}\sqrt{\mathrm{3}}\mathrm{t}\Rightarrow\mathrm{t}=\mathrm{t}' \\ $$$$\mathrm{t}=\mathrm{t}'\:\mathrm{in}\:\mathrm{eq}.\left(\mathrm{iii}\right)\Rightarrow\mathrm{y}−\mathrm{10}=\mathrm{15t}−\mathrm{20t}^{\mathrm{2}} \:…\left(\mathrm{v}\right) \\ $$$$\left(\mathrm{i}\right)+\left(\mathrm{v}\right)\Rightarrow\mathrm{0}=\mathrm{15t}−\mathrm{15t}^{\mathrm{2}} \Rightarrow\mathrm{t}=\mathrm{1}\:\mathrm{sec} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{5}\sqrt{\mathrm{3}}\:,\:\mathrm{y}=\mathrm{5}.\:\:\mathrm{P}\left(\mathrm{5}\sqrt{\mathrm{3}}\:,\:\mathrm{5}\right) \\ $$
Commented by Ar Brandon last updated on 14/Sep/20

Commented by malwan last updated on 14/Sep/20

$${greeeeet} \\ $$$${thanks}\:{alot} \\ $$
Answered by mr W last updated on 15/Sep/20
![position of first bullet: x_1 =u cos θ (t+Δt) y_1 =h+u sin θ (t+Δt)−(1/2)g(t+Δt)^2 position of second bullet: x_2 =ut y_2 =h−(1/2)gt^2 u cos θ (t+Δt)=ut ⇒t+Δt=(t/(cos θ)) h+u sin θ (t+Δt)−(1/2)g(t+Δt)^2 =h−(1/2)gt^2 (t/(cos θ))[u sin θ−((gt)/(2 cos θ))]=−(1/2)gt^2 ⇒t=((2u)/(g tan θ))=((2×5(√3))/(10×(√3)))=1 sec ⇒Δt=((1/(cos θ))−1)((2u)/(g tan θ)) =(2−1)((2×5(√3))/(10×(√3)))=1 sec x=5(√3) y=10−((10)/2)×1^2 =5](https://www.tinkutara.com/question/Q113712.png)
$${position}\:{of}\:{first}\:{bullet}: \\ $$$${x}_{\mathrm{1}} ={u}\:\mathrm{cos}\:\theta\:\left({t}+\Delta{t}\right) \\ $$$${y}_{\mathrm{1}} ={h}+{u}\:\mathrm{sin}\:\theta\:\left({t}+\Delta{t}\right)−\frac{\mathrm{1}}{\mathrm{2}}{g}\left({t}+\Delta{t}\right)^{\mathrm{2}} \\ $$$${position}\:{of}\:{second}\:{bullet}: \\ $$$${x}_{\mathrm{2}} ={ut} \\ $$$${y}_{\mathrm{2}} ={h}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$ \\ $$$${u}\:\mathrm{cos}\:\theta\:\left({t}+\Delta{t}\right)={ut} \\ $$$$\Rightarrow{t}+\Delta{t}=\frac{{t}}{\mathrm{cos}\:\theta} \\ $$$${h}+{u}\:\mathrm{sin}\:\theta\:\left({t}+\Delta{t}\right)−\frac{\mathrm{1}}{\mathrm{2}}{g}\left({t}+\Delta{t}\right)^{\mathrm{2}} ={h}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$\frac{{t}}{\mathrm{cos}\:\theta}\left[{u}\:\mathrm{sin}\:\theta−\frac{{gt}}{\mathrm{2}\:\mathrm{cos}\:\theta}\right]=−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$\Rightarrow{t}=\frac{\mathrm{2}{u}}{{g}\:\mathrm{tan}\:\theta}=\frac{\mathrm{2}×\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{10}×\sqrt{\mathrm{3}}}=\mathrm{1}\:{sec} \\ $$$$\Rightarrow\Delta{t}=\left(\frac{\mathrm{1}}{\mathrm{cos}\:\theta}−\mathrm{1}\right)\frac{\mathrm{2}{u}}{{g}\:\mathrm{tan}\:\theta} \\ $$$$=\left(\mathrm{2}−\mathrm{1}\right)\frac{\mathrm{2}×\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{10}×\sqrt{\mathrm{3}}}=\mathrm{1}\:{sec} \\ $$$$ \\ $$$${x}=\mathrm{5}\sqrt{\mathrm{3}} \\ $$$${y}=\mathrm{10}−\frac{\mathrm{10}}{\mathrm{2}}×\mathrm{1}^{\mathrm{2}} =\mathrm{5} \\ $$
