Menu Close

Two-masses-5-kg-and-M-are-hanging-with-the-help-of-light-rope-and-pulley-as-shown-below-If-the-system-is-in-equilibrium-then-M-

Tinku Tara 0 Comments
Pin




Question Number 17530 by Tinkutara last updated on 07/Jul/17
Two masses 5 kg and M are hanging with the help of light rope and pulley as shown below. If the system is in equilibrium then M =
$$\mathrm{Two}\:\mathrm{masses}\:\mathrm{5}\:\mathrm{kg}\:\mathrm{and}\:{M}\:\mathrm{are}\:\mathrm{hanging} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{help}\:\mathrm{of}\:\mathrm{light}\:\mathrm{rope}\:\mathrm{and}\:\mathrm{pulley} \\ $$$$\mathrm{as}\:\mathrm{shown}\:\mathrm{below}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{system}\:\mathrm{is}\:\mathrm{in} \\ $$$$\mathrm{equilibrium}\:\mathrm{then}\:{M}\:= \\ $$
Commented by Tinkutara last updated on 07/Jul/17
Commented by mrW1 last updated on 07/Jul/17
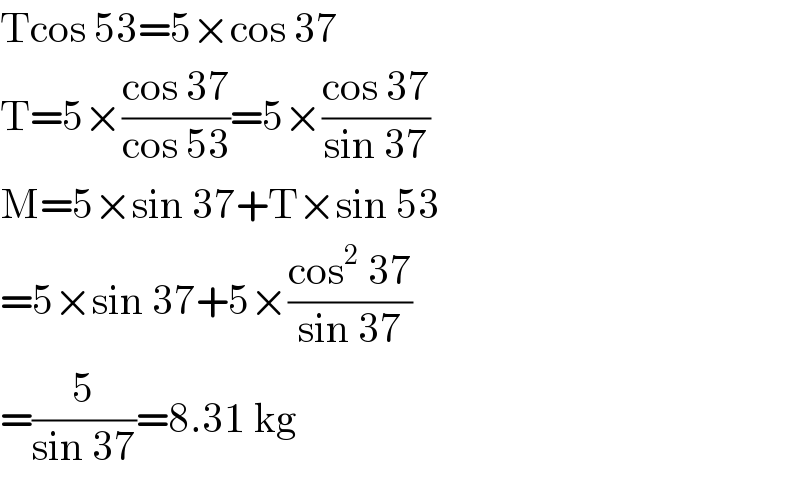
Tcos 53=5×cos 37 T=5×((cos 37)/(cos 53))=5×((cos 37)/(sin 37)) M=5×sin 37+T×sin 53 =5×sin 37+5×((cos^2 37)/(sin 37)) =(5/(sin 37))=8.31 kg
$$\mathrm{Tcos}\:\mathrm{53}=\mathrm{5}×\mathrm{cos}\:\mathrm{37} \\ $$$$\mathrm{T}=\mathrm{5}×\frac{\mathrm{cos}\:\mathrm{37}}{\mathrm{cos}\:\mathrm{53}}=\mathrm{5}×\frac{\mathrm{cos}\:\mathrm{37}}{\mathrm{sin}\:\mathrm{37}} \\ $$$$\mathrm{M}=\mathrm{5}×\mathrm{sin}\:\mathrm{37}+\mathrm{T}×\mathrm{sin}\:\mathrm{53} \\ $$$$=\mathrm{5}×\mathrm{sin}\:\mathrm{37}+\mathrm{5}×\frac{\mathrm{cos}^{\mathrm{2}} \:\mathrm{37}}{\mathrm{sin}\:\mathrm{37}} \\ $$$$=\frac{\mathrm{5}}{\mathrm{sin}\:\mathrm{37}}=\mathrm{8}.\mathrm{31}\:\mathrm{kg} \\ $$
Commented by 1234Hello last updated on 07/Jul/17
Thanks Sir! I forgot the options. But can you explain why M = 5 sin 37° + T sin 53°?
$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{I}\:\mathrm{forgot}\:\mathrm{the}\:\mathrm{options}.\:\mathrm{But} \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{why}\:{M}\:=\:\mathrm{5}\:\mathrm{sin}\:\mathrm{37}° \\ $$$$+\:{T}\:\mathrm{sin}\:\mathrm{53}°? \\ $$
Commented by mrW1 last updated on 07/Jul/17
I don′t understand what you mean with it is not in the options. You can solve it in different ways. Since 37+53=90, the three forces build a right angeled triangle, so you can directly get M=5/sin 37°. If you have no calculator, you can use sin 37≈((sin 30+sin 45)/2)≈((0.5+0.7)/2)=0.6 ⇒M≈5/0.6≈8.3.
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{what}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{with} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{in}\:\mathrm{the}\:\mathrm{options}.\:\mathrm{You}\:\mathrm{can}\:\mathrm{solve} \\ $$$$\mathrm{it}\:\mathrm{in}\:\mathrm{different}\:\mathrm{ways}.\:\mathrm{Since}\:\mathrm{37}+\mathrm{53}=\mathrm{90}, \\ $$$$\mathrm{the}\:\mathrm{three}\:\mathrm{forces}\:\mathrm{build}\:\mathrm{a}\:\mathrm{right}\:\mathrm{angeled} \\ $$$$\mathrm{triangle},\:\mathrm{so}\:\mathrm{you}\:\mathrm{can}\:\mathrm{directly}\:\mathrm{get} \\ $$$$\mathrm{M}=\mathrm{5}/\mathrm{sin}\:\mathrm{37}°.\:\mathrm{If}\:\mathrm{you}\:\mathrm{have}\:\mathrm{no}\:\mathrm{calculator}, \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:\mathrm{sin}\:\mathrm{37}\approx\frac{\mathrm{sin}\:\mathrm{30}+\mathrm{sin}\:\mathrm{45}}{\mathrm{2}}\approx\frac{\mathrm{0}.\mathrm{5}+\mathrm{0}.\mathrm{7}}{\mathrm{2}}=\mathrm{0}.\mathrm{6} \\ $$$$\Rightarrow\mathrm{M}\approx\mathrm{5}/\mathrm{0}.\mathrm{6}\approx\mathrm{8}.\mathrm{3}. \\ $$
Commented by ajfour last updated on 07/Jul/17
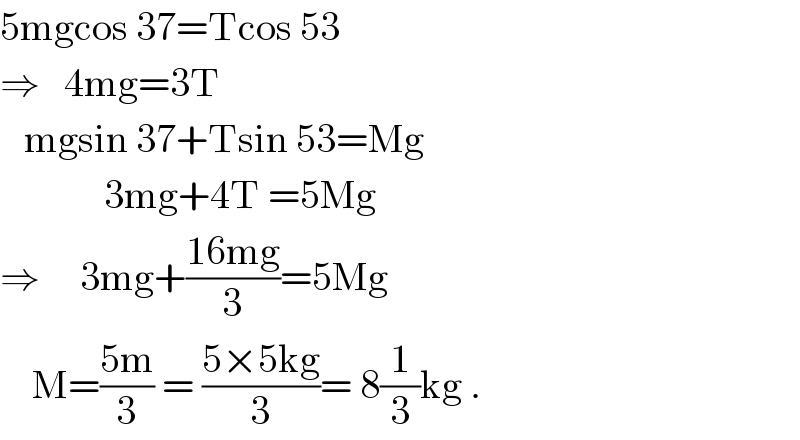
5mgcos 37=Tcos 53 ⇒ 4mg=3T mgsin 37+Tsin 53=Mg 3mg+4T =5Mg ⇒ 3mg+((16mg)/3)=5Mg M=((5m)/3) = ((5×5kg)/3)= 8(1/3)kg .
$$\mathrm{5mgcos}\:\mathrm{37}=\mathrm{Tcos}\:\mathrm{53} \\ $$$$\Rightarrow\:\:\:\mathrm{4mg}=\mathrm{3T} \\ $$$$\:\:\:\mathrm{mgsin}\:\mathrm{37}+\mathrm{Tsin}\:\mathrm{53}=\mathrm{Mg} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3mg}+\mathrm{4T}\:=\mathrm{5Mg} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{3mg}+\frac{\mathrm{16mg}}{\mathrm{3}}=\mathrm{5Mg} \\ $$$$\:\:\:\:\mathrm{M}=\frac{\mathrm{5m}}{\mathrm{3}}\:=\:\frac{\mathrm{5}×\mathrm{5kg}}{\mathrm{3}}=\:\mathrm{8}\frac{\mathrm{1}}{\mathrm{3}}\mathrm{kg}\:. \\ $$
Commented by mrW1 last updated on 07/Jul/17
equilibrium in x−direction: Tcos 53=5×cos 37 equilibrium in y−direction: M=5×sin 37+T×sin 53
$$\mathrm{equilibrium}\:\mathrm{in}\:\mathrm{x}−\mathrm{direction}: \\ $$$$\mathrm{Tcos}\:\mathrm{53}=\mathrm{5}×\mathrm{cos}\:\mathrm{37} \\ $$$$\mathrm{equilibrium}\:\mathrm{in}\:\mathrm{y}−\mathrm{direction}: \\ $$$$\mathrm{M}=\mathrm{5}×\mathrm{sin}\:\mathrm{37}+\mathrm{T}×\mathrm{sin}\:\mathrm{53} \\ $$
Commented by Tinkutara last updated on 08/Jul/17
Thanks ajfour and mrW1 Sir!
$$\mathrm{Thanks}\:\mathrm{ajfour}\:\mathrm{and}\:\mathrm{mrW1}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *