Question Number 181485 by mr W last updated on 25/Nov/22
$${two}\:{medians}\:{of}\:{a}\:{triange}\:{are}\:\mathrm{3}\:{and} \\ $$$$\mathrm{4}\:{cm}\:{respectively}.\:{find}\:{the}\:{maximum} \\ $$$${area}\:{of}\:{the}\:{triangle}. \\ $$
Answered by Acem last updated on 26/Nov/22
Commented by mr W last updated on 26/Nov/22
$${great}! \\ $$
Commented by Acem last updated on 26/Nov/22
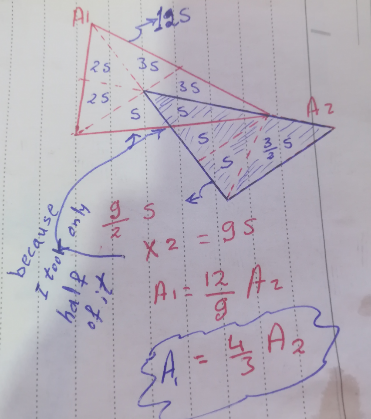
Commented by Acem last updated on 26/Nov/22
$${Thank}\:{you}\:{Sir}! \\ $$$$ \\ $$$${Because}\:{my}\:{English},\:{please}\:{write}\:{an}\:{explanation} \\ $$$$\:{of}\:{the}\:{idea}\:{of}\:{that}\:{ratio}\:\frac{\mathrm{4}}{\mathrm{3}}\:,\:{with}\:{my}\:{thanks} \\ $$
Commented by mr W last updated on 26/Nov/22
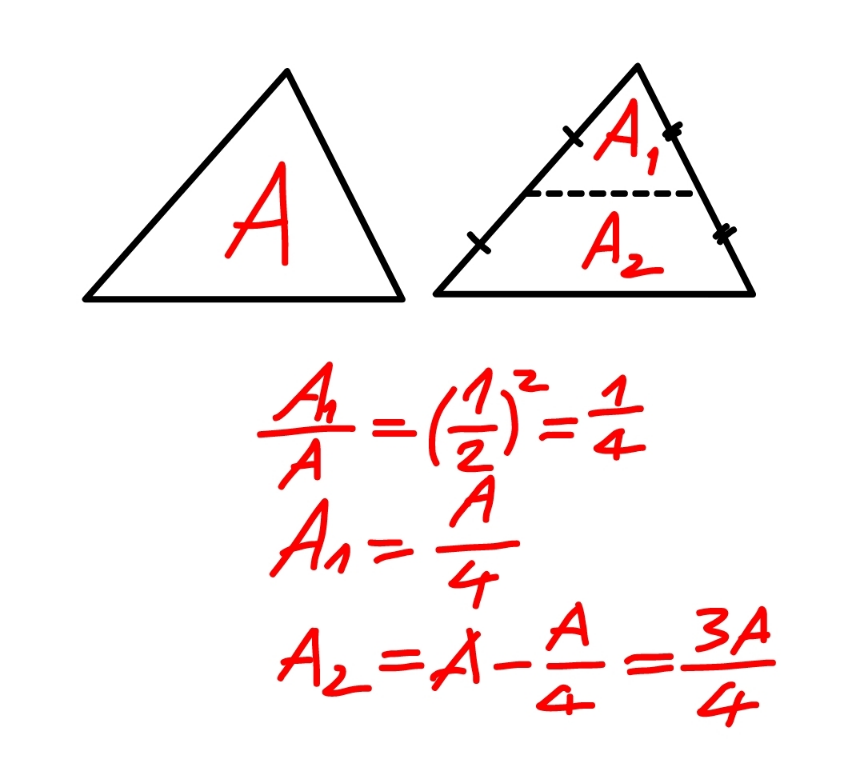
Answered by mr W last updated on 26/Nov/22
Commented by mr W last updated on 26/Nov/22
![say the red medians are given. we know [ΔAFE]=(([ΔABC])/4) ⇒[EFBC]=((3[ΔABC])/4) ⇒[ΔABC]=(4/3)[EFBC] =(4/3)×((m_b m_c sin θ)/2)=((2 m_b m_c sin θ)/3) we see the area of triangle ABC is maximum when θ=90°. [ΔABC]_(max) =((2 m_b m_c )/3)=((2×3×4)/3)=8 cm^2 in this case ΔABC is right angled.](https://www.tinkutara.com/question/Q181500.png)
$${say}\:{the}\:{red}\:{medians}\:{are}\:{given}. \\ $$$${we}\:{know}\:\left[\Delta{AFE}\right]=\frac{\left[\Delta{ABC}\right]}{\mathrm{4}} \\ $$$$\Rightarrow\left[{EFBC}\right]=\frac{\mathrm{3}\left[\Delta{ABC}\right]}{\mathrm{4}} \\ $$$$\Rightarrow\left[\Delta{ABC}\right]=\frac{\mathrm{4}}{\mathrm{3}}\left[{EFBC}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{4}}{\mathrm{3}}×\frac{{m}_{{b}} {m}_{{c}} \mathrm{sin}\:\theta}{\mathrm{2}}=\frac{\mathrm{2}\:{m}_{{b}} {m}_{{c}} \mathrm{sin}\:\theta}{\mathrm{3}} \\ $$$${we}\:{see}\:{the}\:{area}\:{of}\:{triangle}\:{ABC} \\ $$$${is}\:{maximum}\:{when}\:\theta=\mathrm{90}°. \\ $$$$\left[\Delta{ABC}\right]_{{max}} =\frac{\mathrm{2}\:{m}_{{b}} {m}_{{c}} }{\mathrm{3}}=\frac{\mathrm{2}×\mathrm{3}×\mathrm{4}}{\mathrm{3}}=\mathrm{8}\:{cm}^{\mathrm{2}} \\ $$$${in}\:{this}\:{case}\:\Delta{ABC}\:{is}\:{right}\:{angled}. \\ $$
Commented by SEKRET last updated on 26/Nov/22
$$\:\:\boldsymbol{\mathrm{beatiful}}\:\:\boldsymbol{\mathrm{answer}} \\ $$
Commented by Acem last updated on 26/Nov/22
$${I}\:{liked}\:{your}\:{method}\:{more}\:{than}\:{mine},\:{thank}\:{you} \\ $$
Commented by Acem last updated on 26/Nov/22
$$ \\ $$$$\:{mine}\:{gives}\:{the}\:{value}\:{of}\:{the}\:\mathrm{3}{rd}\:{midian}\:{and}\:{it} \\ $$$$\:{show}\:{how}\:{to}\:{convert}\:{the}\:{midians}\:{into}\:{sides}\:{of} \\ $$$$\:{the}\:{new}\:{triangle}\:“{right}\:{one}\:=\:{max}'' \\ $$$$\:{that}'{s}\:{good},\:{but}\:{i}\:{felt}\:{that}\:{it}'{s}\:{a}\:{little}\:{unconvincing}. \\ $$
Commented by mr W last updated on 26/Nov/22
Commented by mr W last updated on 26/Nov/22
$${many}\:{roads}\:{lead}\:{to}\:{Rome}! \\ $$