Question Number 25828 by Tinkutara last updated on 15/Dec/17

$${Two}\:{particles}\:{A}\:{and}\:{B}\:{of}\:{equal}\:{masses} \\ $$$${m}\:{are}\:{tied}\:{with}\:{an}\:{inextensible}\:{string} \\ $$$${of}\:{length}\:\mathrm{2}{l}.\:{The}\:{initial}\:{distance} \\ $$$${between}\:{A}\:{and}\:{B}\:{is}\:{l}.\:{Particle}\:{A}\:{is} \\ $$$${given}\:{speed}\:{v}.\:{Find}\:{the}\:{speed}\:{of} \\ $$$${particle}\:{A}\:{and}\:{B}\:{just}\:{after}\:{the}\:{string} \\ $$$${becomes}\:{taut}. \\ $$
Commented by Tinkutara last updated on 15/Dec/17
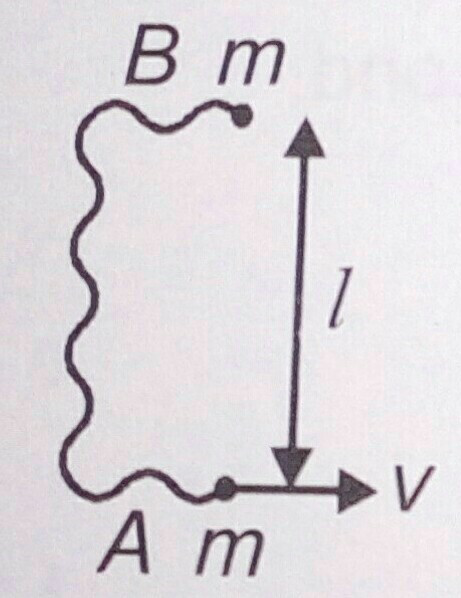
Answered by ajfour last updated on 16/Dec/17
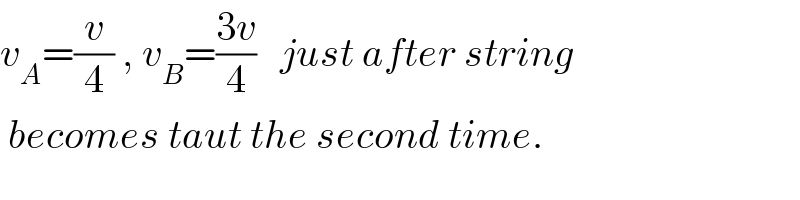
$${v}_{{A}} =\frac{{v}}{\mathrm{4}}\:,\:{v}_{{B}} =\frac{\mathrm{3}{v}}{\mathrm{4}}\:\:\:{just}\:{after}\:{string} \\ $$$$\:{becomes}\:{taut}\:{the}\:{second}\:{time}. \\ $$
Answered by mrW1 last updated on 16/Dec/17
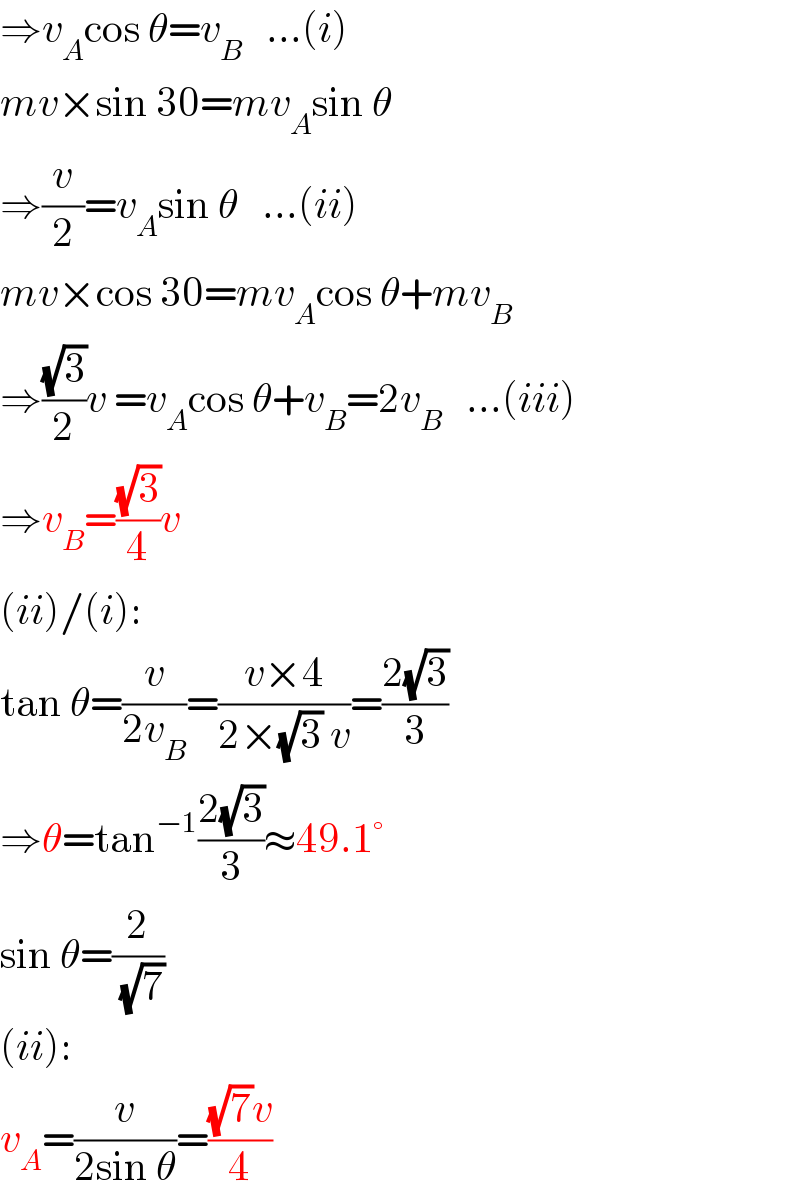
$$\Rightarrow{v}_{{A}} \mathrm{cos}\:\theta={v}_{{B}} \:\:\:…\left({i}\right) \\ $$$${mv}×\mathrm{sin}\:\mathrm{30}={mv}_{{A}} \mathrm{sin}\:\theta \\ $$$$\Rightarrow\frac{{v}}{\mathrm{2}}={v}_{{A}} \mathrm{sin}\:\theta\:\:\:…\left({ii}\right) \\ $$$${mv}×\mathrm{cos}\:\mathrm{30}={mv}_{{A}} \mathrm{cos}\:\theta+{mv}_{{B}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{v}\:={v}_{{A}} \mathrm{cos}\:\theta+{v}_{{B}} =\mathrm{2}{v}_{{B}} \:\:\:…\left({iii}\right) \\ $$$$\Rightarrow{v}_{{B}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{v} \\ $$$$\left({ii}\right)/\left({i}\right): \\ $$$$\mathrm{tan}\:\theta=\frac{{v}}{\mathrm{2}{v}_{{B}} }=\frac{{v}×\mathrm{4}}{\mathrm{2}×\sqrt{\mathrm{3}}\:{v}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\approx\mathrm{49}.\mathrm{1}° \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}}} \\ $$$$\left({ii}\right): \\ $$$${v}_{{A}} =\frac{{v}}{\mathrm{2sin}\:\theta}=\frac{\sqrt{\mathrm{7}}{v}}{\mathrm{4}} \\ $$
Commented by mrW1 last updated on 16/Dec/17
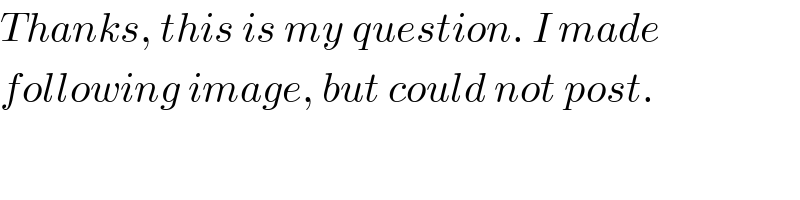
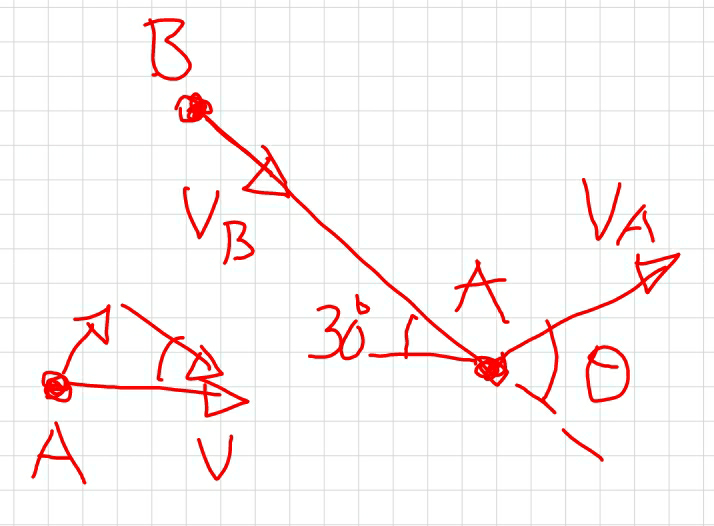
$${Thanks},\:{this}\:{is}\:{my}\:{question}.\:{I}\:{made} \\ $$$${following}\:{image},\:{but}\:{could}\:{not}\:{post}. \\ $$
Commented by Tinkutara last updated on 16/Dec/17
Thank you Sir!
Commented by mrW1 last updated on 16/Dec/17
Commented by ajfour last updated on 16/Dec/17
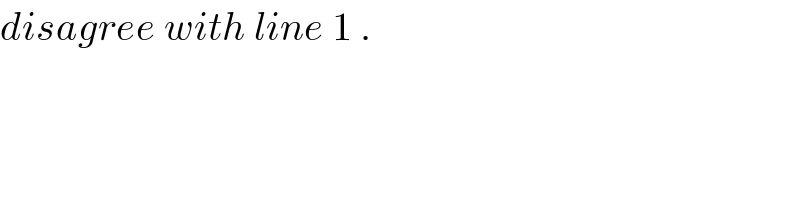
$${disagree}\:{with}\:{line}\:\mathrm{1}\:. \\ $$
Commented by mrW1 last updated on 16/Dec/17

$${after}\:{the}\:{string}\:{is}\:{got}\:{taut},\:{both}\:{articles} \\ $$$${have}\:{the}\:{same}\:{speed}\:{in}\:{the}\:{direction} \\ $$$${of}\:{the}\:{string}.\:{what}\:{is}\:{wrong}? \\ $$
Commented by ajfour last updated on 16/Dec/17
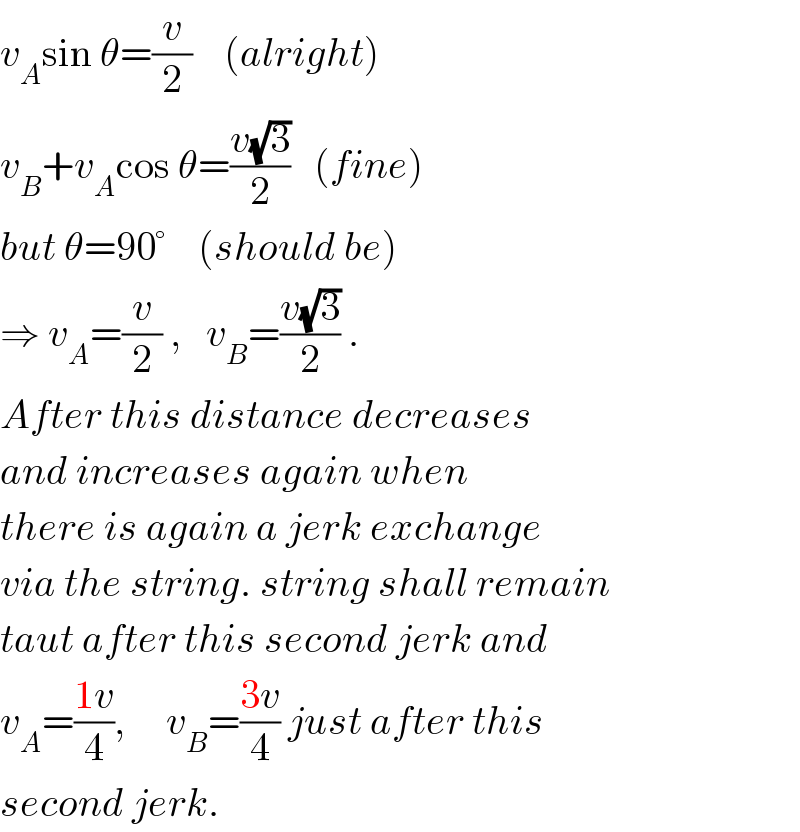
$${v}_{{A}} \mathrm{sin}\:\theta=\frac{{v}}{\mathrm{2}}\:\:\:\:\left({alright}\right) \\ $$$${v}_{{B}} +{v}_{{A}} \mathrm{cos}\:\theta=\frac{{v}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\left({fine}\right) \\ $$$${but}\:\theta=\mathrm{90}°\:\:\:\:\left({should}\:{be}\right) \\ $$$$\Rightarrow\:{v}_{{A}} =\frac{{v}}{\mathrm{2}}\:,\:\:\:{v}_{{B}} =\frac{{v}\sqrt{\mathrm{3}}}{\mathrm{2}}\:. \\ $$$${After}\:{this}\:{distance}\:{decreases} \\ $$$${and}\:{increases}\:{again}\:{when} \\ $$$${there}\:{is}\:{again}\:{a}\:{jerk}\:{exchange} \\ $$$${via}\:{the}\:{string}.\:{string}\:{shall}\:{remain} \\ $$$${taut}\:{after}\:{this}\:{second}\:{jerk}\:{and} \\ $$$${v}_{{A}} =\frac{\mathrm{1}{v}}{\mathrm{4}},\:\:\:\:\:{v}_{{B}} =\frac{\mathrm{3}{v}}{\mathrm{4}}\:{just}\:{after}\:{this}\: \\ $$$${second}\:{jerk}. \\ $$
Commented by ajfour last updated on 16/Dec/17
Commented by ajfour last updated on 16/Dec/17

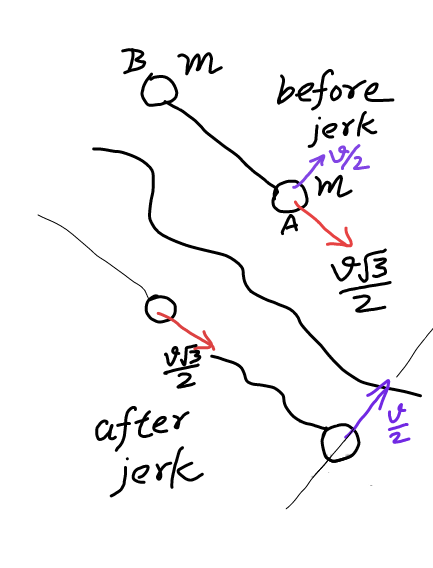
$${it}\:{is}\:{a}\:{string},\:\:{the}\:{velocity} \\ $$$${component}\:{along}\:{the}\:{string} \\ $$$${length}\:{will}\:{be}\:{exchanged}. \\ $$$${v}_{{A}} \left({parallel}\:{to}\:{string}\right)\:=\mathrm{0} \\ $$$${v}_{{B}} =\frac{{v}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\left({along}\:{string}\:{length}\right). \\ $$$${separation}\:{between}\:{A}\:{and}\:{B} \\ $$$${decreases}\:{hereafter}\:{and}\:{when} \\ $$$${again}\:{increases}\:{to}\:\mathrm{2}{l}\:{whereupon} \\ $$$${their}\:{is}\:{another}\:{impulse}\:{exchange} \\ $$$${and}\:{A}\:{and}\:{B}\:{will}\:{come}\:{in}\:{a} \\ $$$${vertical}\:{line}\:{of}\:{plane}\:\left({i}\:{shall}\right. \\ $$$$\left.{post}\:{image}\right).\:{After}\:{this}\: \\ $$$${their}\:{velocities}\:{become}\:{parallel} \\ $$$${to}\:{direction}\:{of}\:{original}\:{velocity} \\ $$$${v}\:\:{with}\:{v}_{{A}} =\frac{\mathrm{1}{v}}{\mathrm{4}}\:\:\:{and}\:\:{v}_{{B}} =\frac{\mathrm{3}{v}}{\mathrm{4}}\:. \\ $$
Commented by ajfour last updated on 16/Dec/17
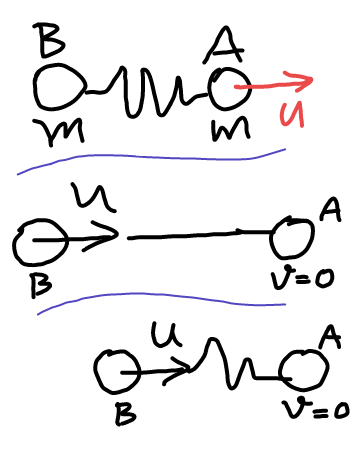
Commented by ajfour last updated on 16/Dec/17
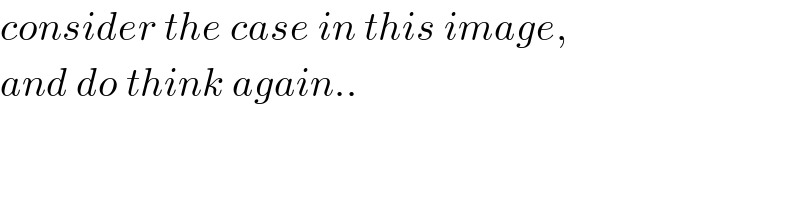
$${consider}\:{the}\:{case}\:{in}\:{this}\:{image}, \\ $$$${and}\:{do}\:{think}\:{again}.. \\ $$
Commented by mrW1 last updated on 16/Dec/17
Commented by mrW1 last updated on 16/Dec/17
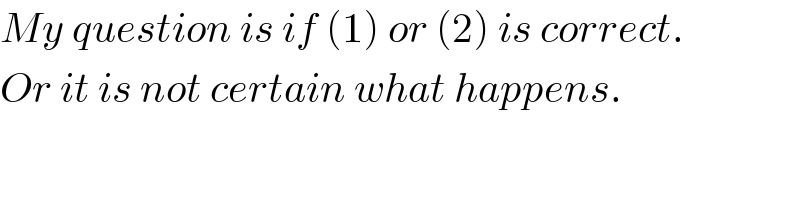
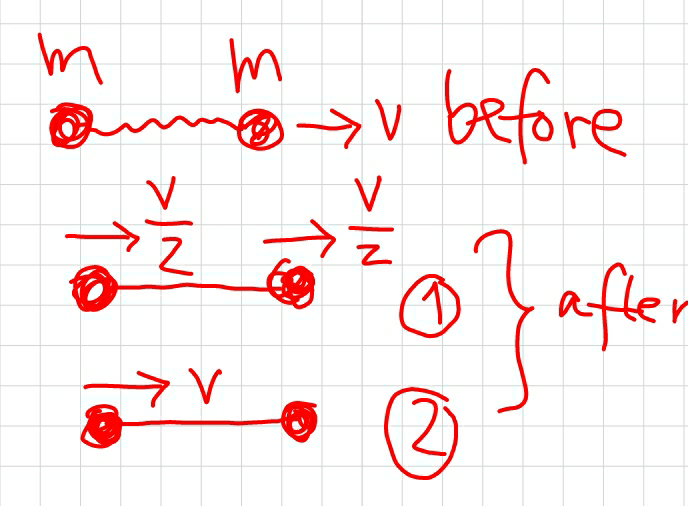
$${My}\:{question}\:{is}\:{if}\:\left(\mathrm{1}\right)\:{or}\:\left(\mathrm{2}\right)\:{is}\:{correct}. \\ $$$${Or}\:{it}\:{is}\:{not}\:{certain}\:{what}\:{happens}. \\ $$
Commented by ajfour last updated on 16/Dec/17

$$\left(\mathrm{2}\right)\:{is}\:{correct}\:. \\ $$
Commented by ajfour last updated on 16/Dec/17
Commented by ajfour last updated on 16/Dec/17

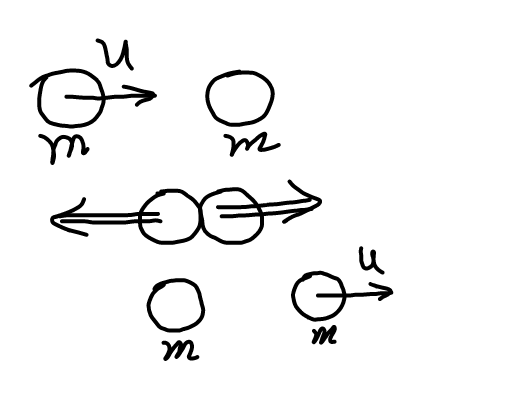
$${If}\:{tied}\:{with}\:{string}\:\left({and}\:{no}\:{energy}\right. \\ $$$$\left.{losses}\right)\:\:{just}\:{the}\:{forces}\:{and} \\ $$$${velocities}\:{will}\:{have}\:{opposite} \\ $$$${directions}. \\ $$
Commented by mrW1 last updated on 16/Dec/17
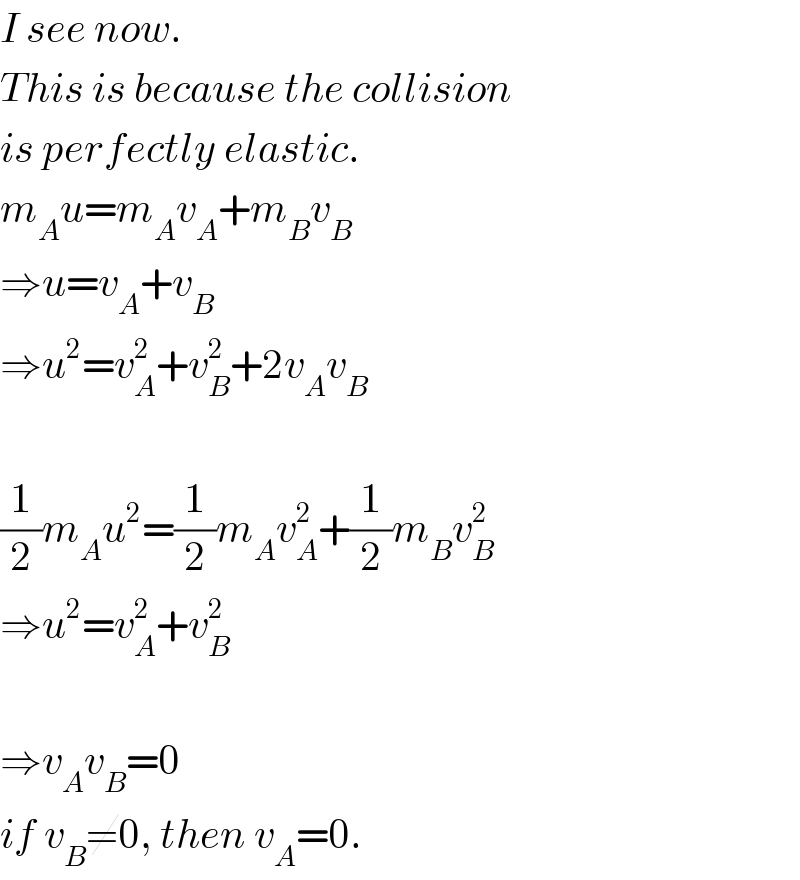
$${I}\:{see}\:{now}. \\ $$$${This}\:{is}\:{because}\:{the}\:{collision} \\ $$$${is}\:{perfectly}\:{elastic}. \\ $$$${m}_{{A}} {u}={m}_{{A}} {v}_{{A}} +{m}_{{B}} {v}_{{B}} \\ $$$$\Rightarrow{u}={v}_{{A}} +{v}_{{B}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} ={v}_{{A}} ^{\mathrm{2}} +{v}_{{B}} ^{\mathrm{2}} +\mathrm{2}{v}_{{A}} {v}_{{B}} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{m}_{{A}} {u}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{m}_{{A}} {v}_{{A}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}_{{B}} {v}_{{B}} ^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} ={v}_{{A}} ^{\mathrm{2}} +{v}_{{B}} ^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow{v}_{{A}} {v}_{{B}} =\mathrm{0} \\ $$$${if}\:{v}_{{B}} \neq\mathrm{0},\:{then}\:{v}_{{A}} =\mathrm{0}. \\ $$
Commented by ajfour last updated on 16/Dec/17

$${thanks}\:{for}\:{the}\:{notice}\:{Sir}! \\ $$
