Question Number 37945 by NECx last updated on 19/Jun/18

$${Two}\:{plane}\:{mirrors}\:{are}\:{inclined}\:{at} \\ $$$${an}\:{angle}\:{of}\:\mathrm{30}°.{A}\:{ray}\:{of}\:{light}\:{which} \\ $$$${makes}\:{an}\:{angle}\:{of}\:{incidence}\:{of}\:\mathrm{50}° \\ $$$${with}\:{one}\:{of}\:{the}\:{mirrors},{undergoes} \\ $$$${two}\:{successive}\:{reflections}\:{at}\:{the} \\ $$$${mirrors}.{Calculate}\:{the}\:{angle}\:{of} \\ $$$${deviation}. \\ $$$$ \\ $$$$ \\ $$$${please}\:{help}….{its}\:{urgent} \\ $$
Commented by MrW3 last updated on 20/Jun/18
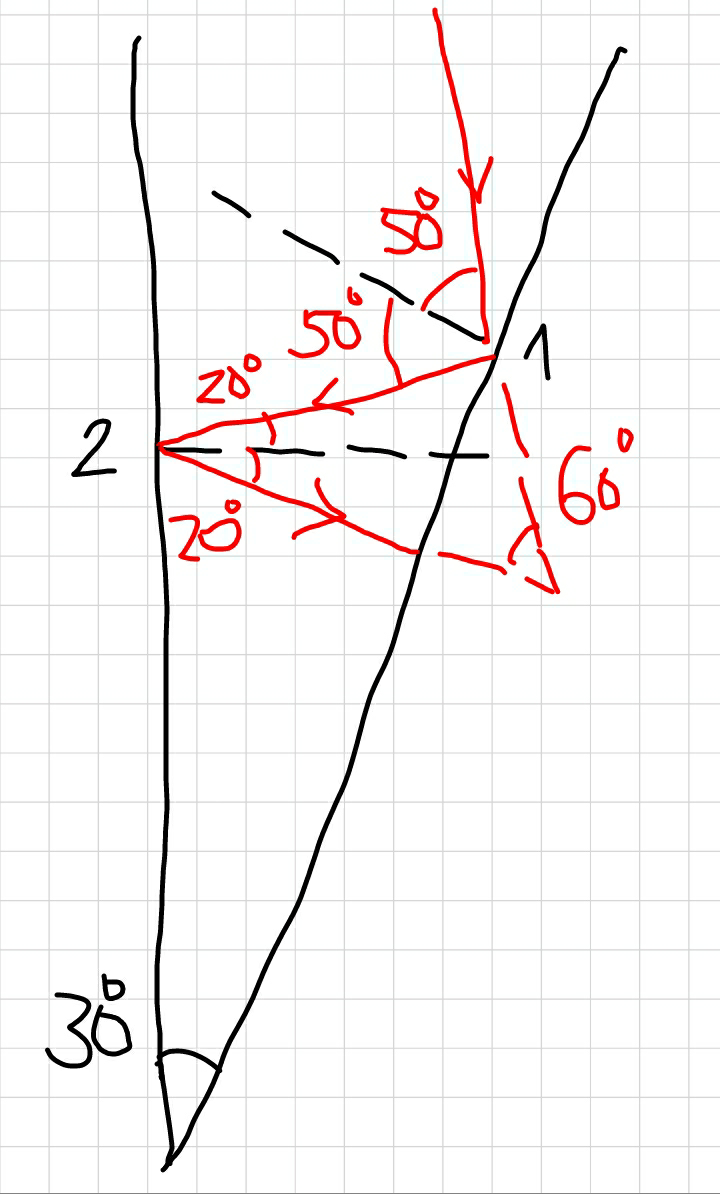
Commented by MrW3 last updated on 20/Jun/18
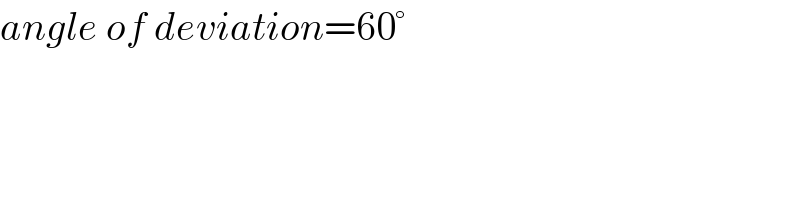
$${angle}\:{of}\:{deviation}=\mathrm{60}° \\ $$
Commented by MrW3 last updated on 20/Jun/18

Commented by MrW3 last updated on 20/Jun/18
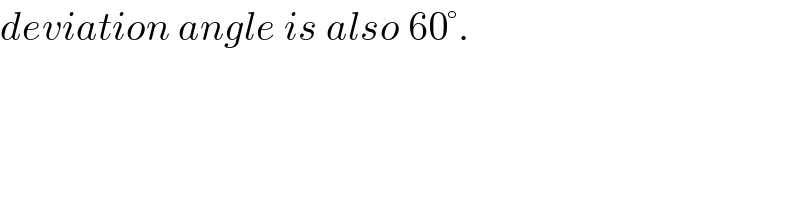
$${deviation}\:{angle}\:{is}\:{also}\:\mathrm{60}°. \\ $$
Commented by NECx last updated on 20/Jun/18
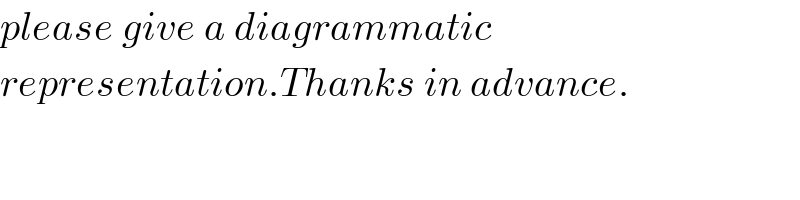
$${please}\:{give}\:{a}\:{diagrammatic} \\ $$$${representation}.{Thanks}\:{in}\:{advance}. \\ $$
Commented by NECx last updated on 20/Jun/18
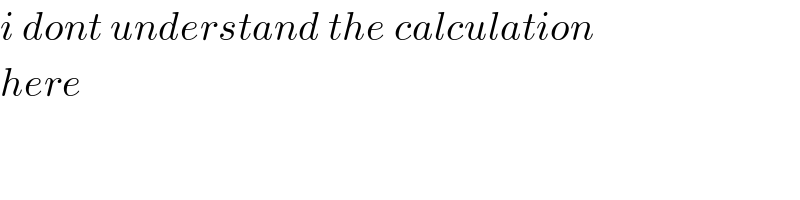
$${i}\:{dont}\:{understand}\:{the}\:{calculation} \\ $$$${here} \\ $$
Commented by MrW3 last updated on 21/Jun/18

Commented by MrW3 last updated on 21/Jun/18

$${deviation}\:{angle}\:{means}\:{the}\:{change}\:{of} \\ $$$${direction}. \\ $$$${to}\:{calculate}\:{it},\:{you}\:{can}\:{take}\:{an}\:{any} \\ $$$${reference}\:{line}\:{and}\:{determine}\:{the} \\ $$$${angle}\:{between}\:{the}\:{light}\:{ray}\:{and}\:{the} \\ $$$${reference}\:{line}\:{before}\:{the}\:{reflections} \\ $$$${and}\:{after}\:{the}\:{reflections},\:{the}\:{difference} \\ $$$${of}\:{both}\:{angles}\:{is}\:{then}\:{the}\:{requested} \\ $$$${deviation}\:{angle}. \\ $$
Commented by NECx last updated on 22/Jun/18

$${Thank}\:{you}\:{so}\:{much}.{I}\:{really} \\ $$$${understand}\:{the}\:{concept}\:{now}. \\ $$
Commented by MrW3 last updated on 23/Jun/18
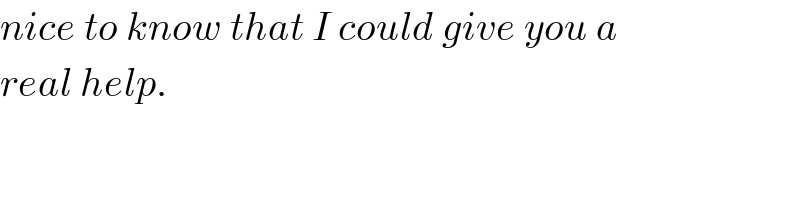
$${nice}\:{to}\:{know}\:{that}\:{I}\:{could}\:{give}\:{you}\:{a} \\ $$$${real}\:{help}. \\ $$
