Question Number 50994 by peter frank last updated on 23/Dec/18
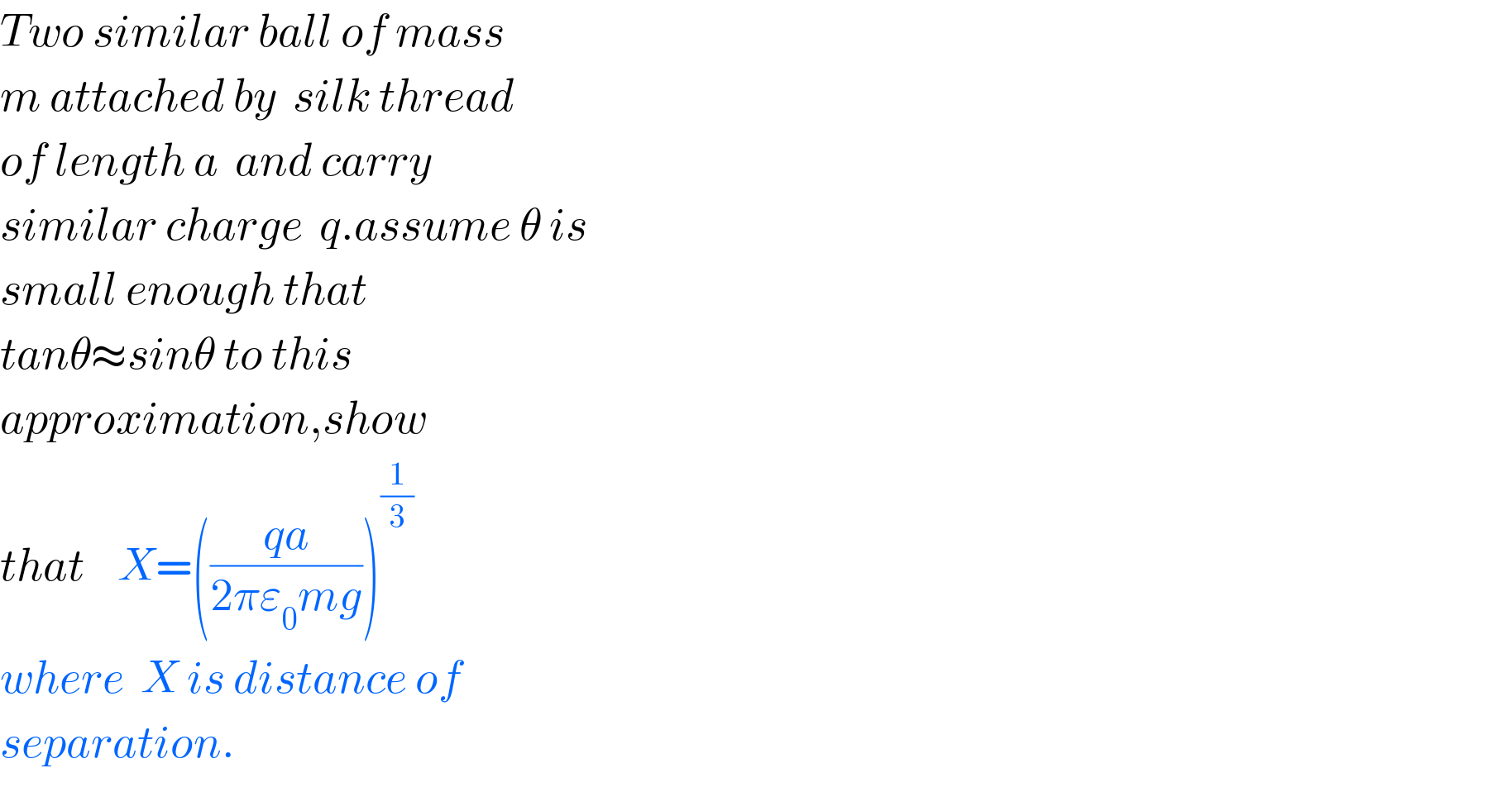
$${Two}\:{similar}\:{ball}\:{of}\:{mass} \\ $$$${m}\:{attached}\:{by}\:\:{silk}\:{thread} \\ $$$${of}\:{length}\:{a}\:\:{and}\:{carry} \\ $$$${similar}\:{charge}\:\:{q}.{assume}\:\theta\:{is} \\ $$$${small}\:{enough}\:{that} \\ $$$${tan}\theta\approx{sin}\theta\:{to}\:{this} \\ $$$${approximation},{show}\: \\ $$$${that}\:\:\:\:{X}=\left(\frac{{qa}}{\mathrm{2}\pi\varepsilon_{\mathrm{0}} {mg}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \: \\ $$$${where}\:\:{X}\:{is}\:{distance}\:{of} \\ $$$${separation}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

$${T}={tension}\:{in}\:{thread}\: \\ $$$${Tcos}\theta={mg} \\ $$$${Tsin}\theta={F}\: \\ $$$${F}={repulsive}\:{force}\:=\frac{\mathrm{1}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\frac{{q}^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$${tan}\theta=\frac{{F}}{{mg}} \\ $$$${sin}\theta=\frac{{F}}{{mg}} \\ $$$$\frac{{x}}{\mathrm{2}{a}}=\frac{\mathrm{1}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }×\frac{{q}^{\mathrm{2}} }{{x}^{\mathrm{2}} }×\frac{\mathrm{1}}{{mg}} \\ $$$${x}^{\mathrm{3}} =\frac{{aq}^{\mathrm{2}} }{\mathrm{2}\pi\epsilon_{\mathrm{0}} }×\frac{\mathrm{1}}{{mg}} \\ $$$${x}=\left(\frac{{aq}^{\mathrm{2}} }{\mathrm{2}\pi\epsilon_{\mathrm{0}} {mg}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$
Answered by peter frank last updated on 23/Dec/18
![F=(q^2 /(4πε_0 r^2 )) [q_1 =q_(2 ) ] sin θ=(x/(2a)) tan θ=(F/(mg)) F=mgtan θ tan θ≈sin θ=θ F=mg(x/(2a))......(i) F=(q^2 /(4πε_0 r^2 )) [ r=x].....(ii) mg(x/(2a))=(q^2 /(4πε_0 x^2 )) x=[((q^2 a)/(4πε_0 mg))]^(1/3)](https://www.tinkutara.com/question/Q51101.png)
$${F}=\frac{{q}^{\mathrm{2}} }{\mathrm{4}\pi\varepsilon_{\mathrm{0}} {r}^{\mathrm{2}} }\:\:\:\left[{q}_{\mathrm{1}} ={q}_{\mathrm{2}\:\:} \right] \\ $$$$\mathrm{sin}\:\theta=\frac{{x}}{\mathrm{2}{a}} \\ $$$$\mathrm{tan}\:\theta=\frac{{F}}{{mg}} \\ $$$${F}={mg}\mathrm{tan}\:\theta \\ $$$$\mathrm{tan}\:\theta\approx\mathrm{sin}\:\theta=\theta \\ $$$${F}={mg}\frac{{x}}{\mathrm{2}{a}}……\left({i}\right) \\ $$$${F}=\frac{{q}^{\mathrm{2}} }{\mathrm{4}\pi\varepsilon_{\mathrm{0}} {r}^{\mathrm{2}} }\:\:\left[\:\:\:{r}={x}\right]…..\left({ii}\right) \\ $$$${mg}\frac{{x}}{\mathrm{2}{a}}=\frac{{q}^{\mathrm{2}} }{\mathrm{4}\pi\varepsilon_{\mathrm{0}} {x}^{\mathrm{2}} } \\ $$$${x}=\left[\frac{{q}^{\mathrm{2}} {a}}{\mathrm{4}\pi\varepsilon_{\mathrm{0}} {mg}}\right]^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$
