Two-similar-spheres-of-the-same-material-have-masses-of-12kg-and250kg-respectively-find-the-radius-of-the-smaller-sphere-if-the-radius-of-the-bigger-shere-is-12-5cm-

Question Number 55918 by imamu222 last updated on 06/Mar/19

T w o s i m i l a r s p h e r e s o f t h e s a m e m a t e r i a l h a v e m a s s e s o f 12 k g a n d 250 k g r e s p e c t i v e l y . f i n d t h e r a d i u s o f t h e s m a l l e r s p h e r e i f t h e r a d i u s o f t h e b i g g e r s h e r e i s 12.5 c m

Answered by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19

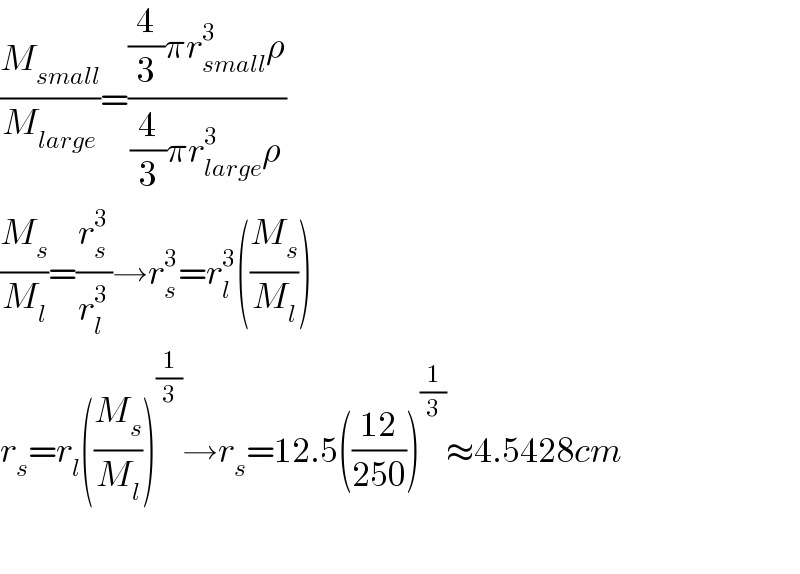
\frac{M_{s m a l l}}{M_{l a r g e}} = \frac{\frac{4}{3} π r_{s m a l l}^{3} ρ}{\frac{4}{3} π r_{l a r g e}^{3} ρ}

\frac{M_{s}}{M_{l}} = \frac{r_{s}^{3}}{r_{l}^{3}} \to r_{s}^{3} = r_{l}^{3} (\frac{M_{s}}{M_{l}})

r_{s} = r_{l} {(\frac{M_{s}}{M_{l}})}^{\frac{1}{3}} \to r_{s} = 12.5 {(\frac{12}{250})}^{\frac{1}{3}} \approx 4.5428 c m