Question Number 184048 by cortano1 last updated on 02/Jan/23
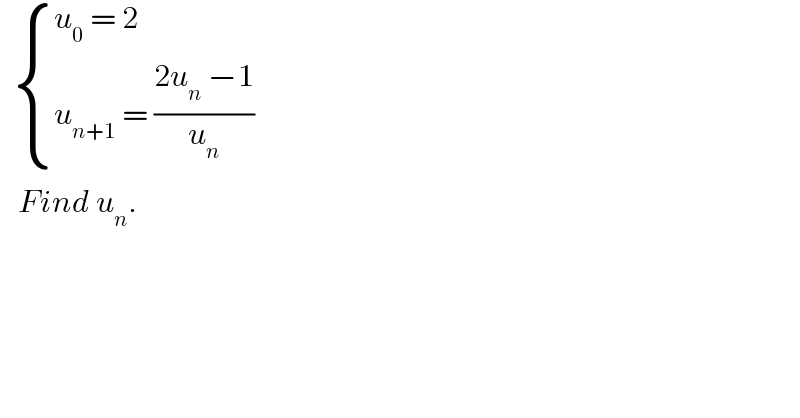
$$\:\:\begin{cases}{{u}_{\mathrm{0}} \:=\:\mathrm{2}}\\{{u}_{{n}+\mathrm{1}} \:=\:\frac{\mathrm{2}{u}_{{n}} \:−\mathrm{1}}{{u}_{{n}} }}\end{cases} \\ $$$$\:\:\:{Find}\:{u}_{{n}} . \\ $$
Answered by SEKRET last updated on 02/Jan/23

$$\:\:\boldsymbol{\mathrm{n}}=\mathrm{0}\:\:\:\:\:\boldsymbol{\mathrm{u}}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\boldsymbol{\mathrm{n}}=\mathrm{1}\:\:\:\:\:\:\boldsymbol{\mathrm{u}}_{\mathrm{2}} \:=\:\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\boldsymbol{\mathrm{n}}=\mathrm{2}\:\:\:\:\:\:\boldsymbol{\mathrm{u}}_{\mathrm{3}} =\:\frac{\mathrm{5}}{\mathrm{4}}\:\:\:\:\:\:\boldsymbol{\mathrm{n}}\:=\:\mathrm{3}\:\:\:\:\boldsymbol{\mathrm{u}}_{\mathrm{4}} =\:\:\frac{\mathrm{6}}{\mathrm{5}} \\ $$$$\:\boldsymbol{\mathrm{n}}=\mathrm{4}\:\:\:\boldsymbol{\mathrm{u}}_{\mathrm{5}} =\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{1}};\:\frac{\mathrm{3}}{\mathrm{2}};\frac{\mathrm{4}}{\mathrm{3}}\:;\frac{\mathrm{5}}{\mathrm{4}};\frac{\mathrm{6}}{\mathrm{5}};\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\:\:\boldsymbol{\mathrm{U}}_{\boldsymbol{\mathrm{n}}} =\:\frac{\boldsymbol{\mathrm{n}}+\mathrm{2}}{\boldsymbol{\mathrm{n}}+\mathrm{1}}\:\: \\ $$$$\:\boldsymbol{{ABDULAZIZ}}\:\:\:\boldsymbol{{ABDUVALIYEV}} \\ $$
Commented by mr W last updated on 02/Jan/23
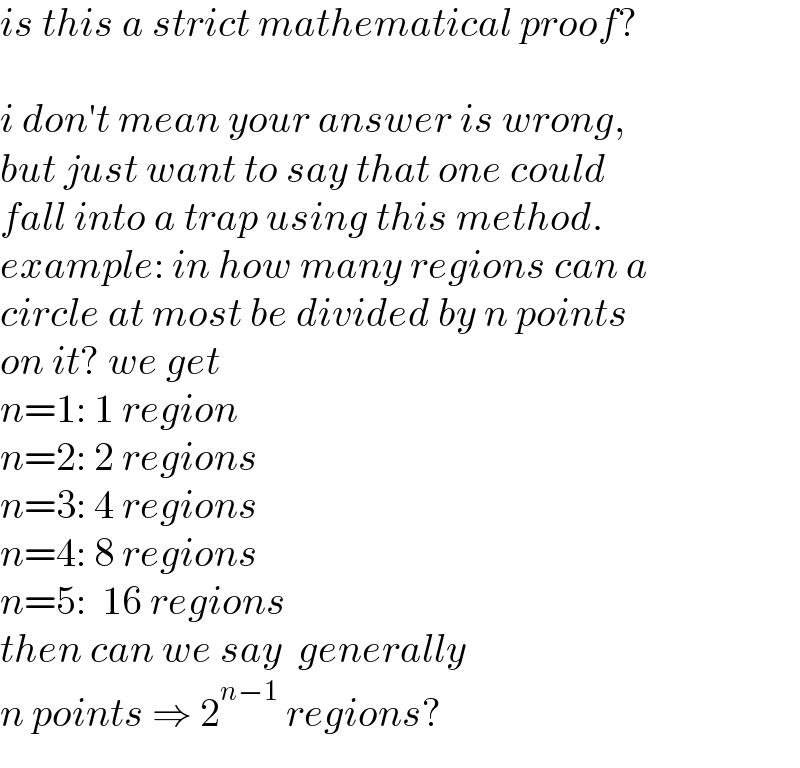
$${is}\:{this}\:{a}\:{strict}\:{mathematical}\:{proof}? \\ $$$$ \\ $$$${i}\:{don}'{t}\:{mean}\:{your}\:{answer}\:{is}\:{wrong}, \\ $$$${but}\:{just}\:{want}\:{to}\:{say}\:{that}\:{one}\:{could}\: \\ $$$${fall}\:{into}\:{a}\:{trap}\:{using}\:{this}\:{method}.\: \\ $$$${example}:\:{in}\:{how}\:{many}\:{regions}\:{can}\:{a}\: \\ $$$${circle}\:{at}\:{most}\:{be}\:{divided}\:{by}\:{n}\:{points}\: \\ $$$${on}\:{it}?\:{we}\:{get} \\ $$$${n}=\mathrm{1}:\:\mathrm{1}\:{region} \\ $$$${n}=\mathrm{2}:\:\mathrm{2}\:{regions} \\ $$$${n}=\mathrm{3}:\:\mathrm{4}\:{regions} \\ $$$${n}=\mathrm{4}:\:\mathrm{8}\:{regions} \\ $$$${n}=\mathrm{5}:\:\:\mathrm{16}\:{regions} \\ $$$${then}\:{can}\:{we}\:{say}\:\:{generally}\: \\ $$$${n}\:{points}\:\Rightarrow\:\mathrm{2}^{{n}−\mathrm{1}} \:{regions}? \\ $$
Commented by Acem last updated on 02/Jan/23
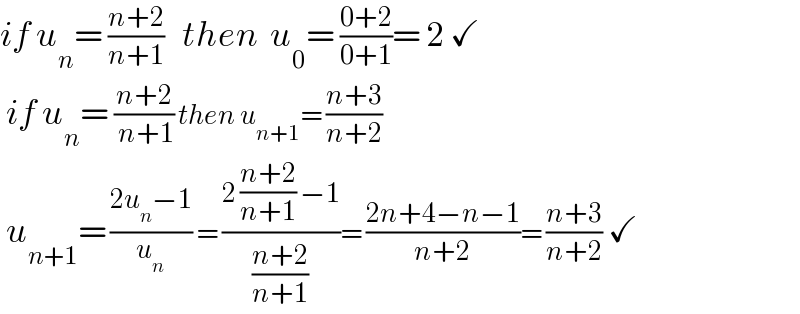
$${if}\:{u}_{{n}} =\:\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}\:\:\:{then}\:\:{u}_{\mathrm{0}} =\:\frac{\mathrm{0}+\mathrm{2}}{\mathrm{0}+\mathrm{1}}=\:\mathrm{2}\:\checkmark \\ $$$$\:{if}\:{u}_{{n}} =\:\frac{{n}+\mathrm{2}}{\:{n}+\mathrm{1}}\:{then}\:{u}_{{n}+\mathrm{1}} =\:\frac{{n}+\mathrm{3}}{{n}+\mathrm{2}}\: \\ $$$$\:{u}_{{n}+\mathrm{1}} =\:\frac{\mathrm{2}{u}_{{n}} −\mathrm{1}}{{u}_{{n}} }\:=\:\frac{\mathrm{2}\:\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}\:−\mathrm{1}}{\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}}=\:\frac{\mathrm{2}{n}+\mathrm{4}−{n}−\mathrm{1}}{{n}+\mathrm{2}}=\:\frac{{n}+\mathrm{3}}{{n}+\mathrm{2}}\:\checkmark \\ $$
Commented by mr W last updated on 02/Jan/23

$${nice}\:{sir}! \\ $$$${this}\:{is}\:{a}\:{strict}\:{proof}\:{for}\:{u}_{{n}} =\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}} \\ $$$${when}\:{we}\:{already}\:{know}\:{u}_{{n}} =\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}. \\ $$$${but}\:{how}\:{to}\:{find}\:{u}_{{n}} \:{generally}?\:{let}'{s} \\ $$$${say}\:{u}_{\mathrm{0}} ={c}.\:{c}\:{could}\:{be}\:{any}\:{real}\:{value}. \\ $$
Commented by SEKRET last updated on 02/Jan/23

$$\boldsymbol{\mathrm{thanks}}\:\:\boldsymbol{\mathrm{sir}}.\:\: \\ $$
Commented by Acem last updated on 02/Jan/23
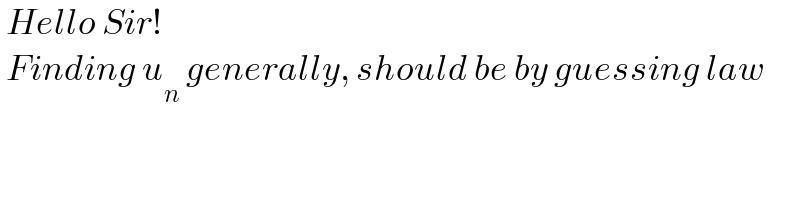
$$\:{Hello}\:{Sir}! \\ $$$$\:{Finding}\:{u}_{{n}} \:{generally},\:{should}\:{be}\:{by}\:{guessing}\:{law} \\ $$
Commented by mr W last updated on 02/Jan/23
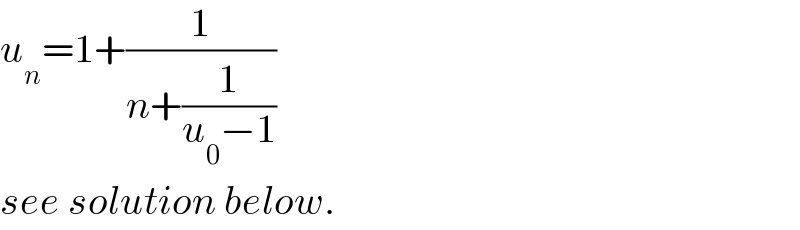
$${u}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{{u}_{\mathrm{0}} −\mathrm{1}}} \\ $$$${see}\:{solution}\:{below}. \\ $$
Answered by cortano2 last updated on 02/Jan/23

$${u}_{\mathrm{0}} =\mathrm{2} \\ $$$${u}_{\mathrm{1}} =\mathrm{3}/\mathrm{2} \\ $$$${u}_{\mathrm{2}} =\mathrm{4}/\mathrm{3} \\ $$$${u}_{\mathrm{3}} =\mathrm{5}/\mathrm{4} \\ $$$${u}_{{n}} =\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}} \\ $$
Commented by mr W last updated on 02/Jan/23
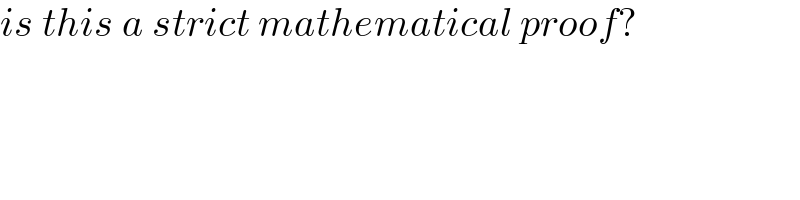
$${is}\:{this}\:{a}\:{strict}\:{mathematical}\:{proof}? \\ $$
Commented by Acem last updated on 02/Jan/23
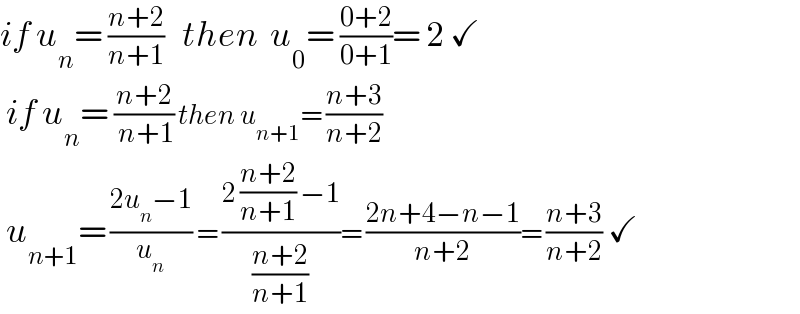
$${if}\:{u}_{{n}} =\:\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}\:\:\:{then}\:\:{u}_{\mathrm{0}} =\:\frac{\mathrm{0}+\mathrm{2}}{\mathrm{0}+\mathrm{1}}=\:\mathrm{2}\:\checkmark \\ $$$$\:{if}\:{u}_{{n}} =\:\frac{{n}+\mathrm{2}}{\:{n}+\mathrm{1}}\:{then}\:{u}_{{n}+\mathrm{1}} =\:\frac{{n}+\mathrm{3}}{{n}+\mathrm{2}}\: \\ $$$$\:{u}_{{n}+\mathrm{1}} =\:\frac{\mathrm{2}{u}_{{n}} −\mathrm{1}}{{u}_{{n}} }\:=\:\frac{\mathrm{2}\:\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}\:−\mathrm{1}}{\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}}=\:\frac{\mathrm{2}{n}+\mathrm{4}−{n}−\mathrm{1}}{{n}+\mathrm{2}}=\:\frac{{n}+\mathrm{3}}{{n}+\mathrm{2}}\:\checkmark \\ $$
Answered by a.lgnaoui last updated on 02/Jan/23
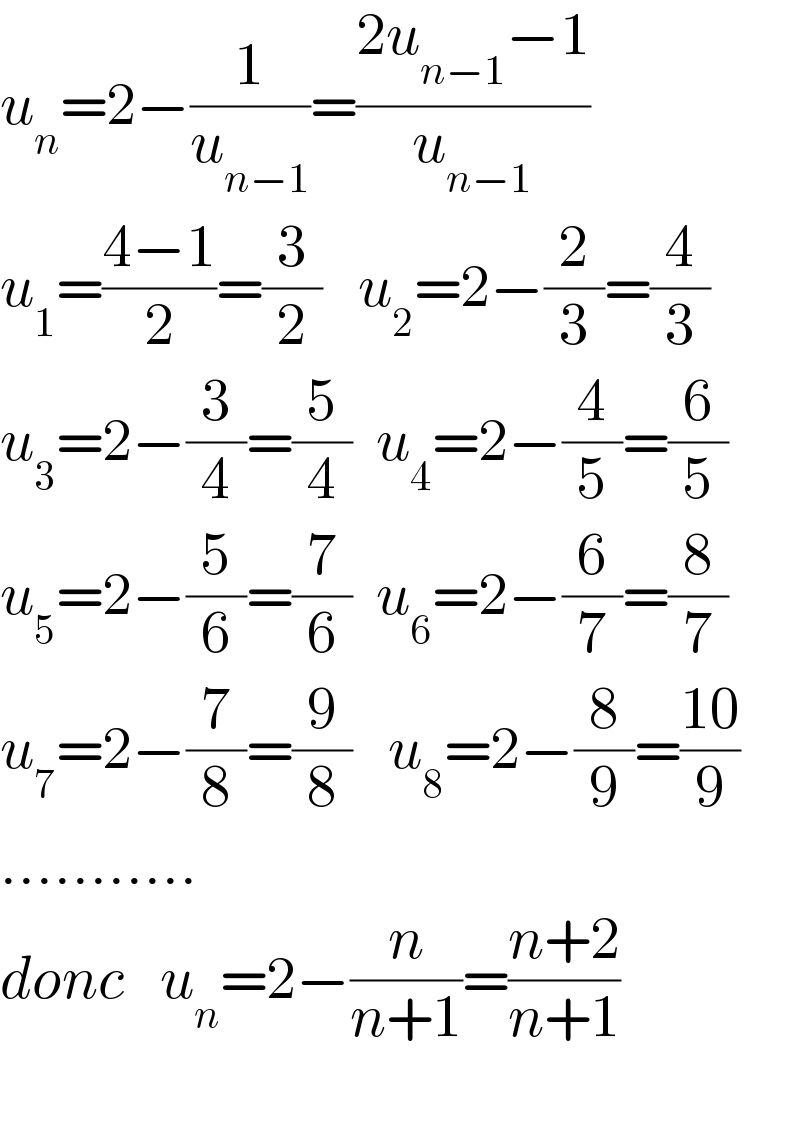
$${u}_{{n}} =\mathrm{2}−\frac{\mathrm{1}}{{u}_{{n}−\mathrm{1}} }=\frac{\mathrm{2}{u}_{{n}−\mathrm{1}} −\mathrm{1}}{{u}_{{n}−\mathrm{1}} } \\ $$$${u}_{\mathrm{1}} =\frac{\mathrm{4}−\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:{u}_{\mathrm{2}} =\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${u}_{\mathrm{3}} =\mathrm{2}−\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{5}}{\mathrm{4}}\:\:{u}_{\mathrm{4}} =\mathrm{2}−\frac{\mathrm{4}}{\mathrm{5}}=\frac{\mathrm{6}}{\mathrm{5}} \\ $$$${u}_{\mathrm{5}} =\mathrm{2}−\frac{\mathrm{5}}{\mathrm{6}}=\frac{\mathrm{7}}{\mathrm{6}}\:\:{u}_{\mathrm{6}} =\mathrm{2}−\frac{\mathrm{6}}{\mathrm{7}}=\frac{\mathrm{8}}{\mathrm{7}} \\ $$$${u}_{\mathrm{7}} =\mathrm{2}−\frac{\mathrm{7}}{\mathrm{8}}=\frac{\mathrm{9}}{\mathrm{8}}\:\:\:{u}_{\mathrm{8}} =\mathrm{2}−\frac{\mathrm{8}}{\mathrm{9}}=\frac{\mathrm{10}}{\mathrm{9}} \\ $$$$……….. \\ $$$${donc}\:\:\:{u}_{{n}} =\mathrm{2}−\frac{{n}}{{n}+\mathrm{1}}=\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}} \\ $$$$ \\ $$
Answered by CrispyXYZ last updated on 02/Jan/23

$${u}_{{n}} =\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}} \\ $$$$\mathrm{Proof}\:\mathrm{with}\:\boldsymbol{\mathrm{Mathematical}}\:\boldsymbol{\mathrm{Induction}} \\ $$$$\left(\mathrm{1}\right)\:{n}=\mathrm{0} \\ $$$${u}_{\mathrm{0}} =\frac{\mathrm{2}}{\mathrm{1}}=\mathrm{2} \\ $$$$\left(\mathrm{2}\right)\:{n}={k}\:\Rightarrow\:{n}={k}+\mathrm{1} \\ $$$${u}_{{k}} =\frac{{k}+\mathrm{2}}{{k}+\mathrm{1}} \\ $$$${u}_{{k}+\mathrm{1}} =\frac{\mathrm{2}{u}_{{k}} −\mathrm{1}}{{u}_{{k}} }=\mathrm{2}−\frac{{k}+\mathrm{1}}{{k}+\mathrm{2}}=\frac{{k}+\mathrm{3}}{{k}+\mathrm{2}}=\frac{\left({k}+\mathrm{1}\right)+\mathrm{2}}{\left({k}+\mathrm{1}\right)+\mathrm{1}} \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{2}\right)\:\Rightarrow\:{u}_{{n}} =\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}\:\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{n} \\ $$
Answered by mr W last updated on 02/Jan/23

$${u}_{{n}+\mathrm{1}} =\frac{\mathrm{2}{u}_{{n}} −\mathrm{1}}{{u}_{{n}} } \\ $$$${u}_{{n}+\mathrm{1}} −\mathrm{1}=\frac{{u}_{{n}} −\mathrm{1}}{{u}_{{n}} } \\ $$$$\frac{\mathrm{1}}{{u}_{{n}+\mathrm{1}} −\mathrm{1}}=\frac{{u}_{{n}} }{{u}_{{n}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{u}_{{n}+\mathrm{1}} −\mathrm{1}}=\mathrm{1}+\frac{\mathrm{1}}{{u}_{{n}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{u}_{{n}+\mathrm{1}} −\mathrm{1}}−\frac{\mathrm{1}}{{u}_{{n}} −\mathrm{1}}=\mathrm{1} \\ $$$${let}\:{A}_{{n}} =\frac{\mathrm{1}}{{u}_{{n}} −\mathrm{1}} \\ $$$${A}_{{n}+\mathrm{1}} −{A}_{{n}} =\mathrm{1}\:\Rightarrow\:{A}.{P}. \\ $$$${A}_{{n}} −{A}_{{n}−\mathrm{1}} =\mathrm{1} \\ $$$$… \\ $$$${A}_{\mathrm{2}} −{A}_{\mathrm{1}} =\mathrm{1} \\ $$$${A}_{\mathrm{1}} −{A}_{\mathrm{0}} =\mathrm{1} \\ $$$$\Rightarrow{A}_{{n}} −{A}_{\mathrm{0}} ={n} \\ $$$$\Rightarrow{A}_{{n}} ={A}_{\mathrm{0}} +{n} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{u}_{{n}} −\mathrm{1}}=\frac{\mathrm{1}}{{u}_{\mathrm{0}} −\mathrm{1}}+{n} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{{u}_{\mathrm{0}} −\mathrm{1}}} \\ $$$${in}\:{case}\:{u}_{\mathrm{0}} =\mathrm{2}: \\ $$$${u}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{{n}+\mathrm{1}}=\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}} \\ $$
Commented by Acem last updated on 02/Jan/23

$${Nice}\:{Sir}!\:{thanks} \\ $$$$\:{question},\:{bec}\:{my}\:{Eng}.\:{what}'{s}\:{A}.{P}. \\ $$
Commented by cortano1 last updated on 03/Jan/23
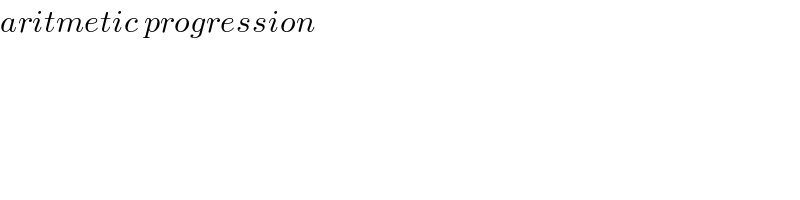
$${aritmetic}\:{progression} \\ $$
Commented by mr W last updated on 03/Jan/23

$${A}.{P}.={arithmethic}\:{progression} \\ $$$${G}.{P}.={geometric}\:{progression} \\ $$
Commented by Acem last updated on 04/Jan/23

$${Thx}\:{friends}! \\ $$
