Question Number 36922 by maxmathsup by imad last updated on 07/Jun/18
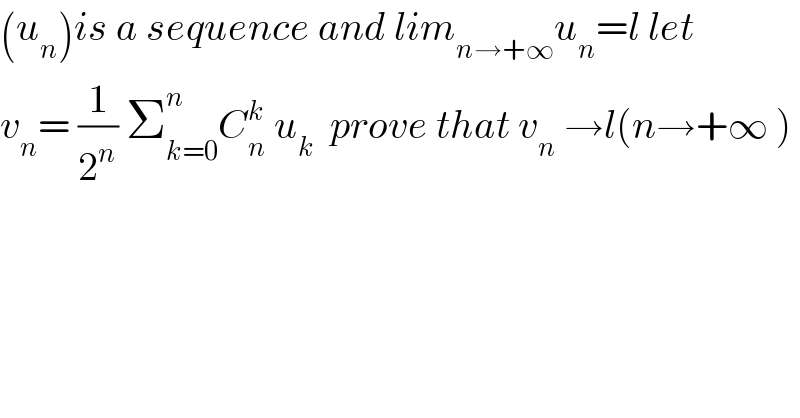
$$\left({u}_{{n}} \right){is}\:{a}\:{sequence}\:{and}\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} ={l}\:{let} \\ $$$${v}_{{n}} =\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} \:{u}_{{k}} \:\:{prove}\:{that}\:{v}_{{n}} \:\rightarrow{l}\left({n}\rightarrow+\infty\:\right) \\ $$
Commented by math khazana by abdo last updated on 10/Jun/18
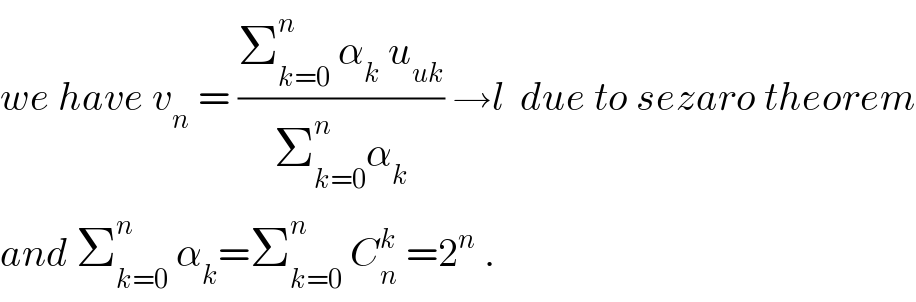
$${we}\:{have}\:{v}_{{n}} \:=\:\frac{\sum_{{k}=\mathrm{0}} ^{{n}} \:\alpha_{{k}} \:{u}_{{uk}} }{\sum_{{k}=\mathrm{0}} ^{{n}} \alpha_{{k}} }\:\rightarrow{l}\:\:{due}\:{to}\:{sezaro}\:{theorem} \\ $$$${and}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\alpha_{{k}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:=\mathrm{2}^{{n}} \:. \\ $$
