Question Number 64650 by mathmax by abdo last updated on 20/Jul/19
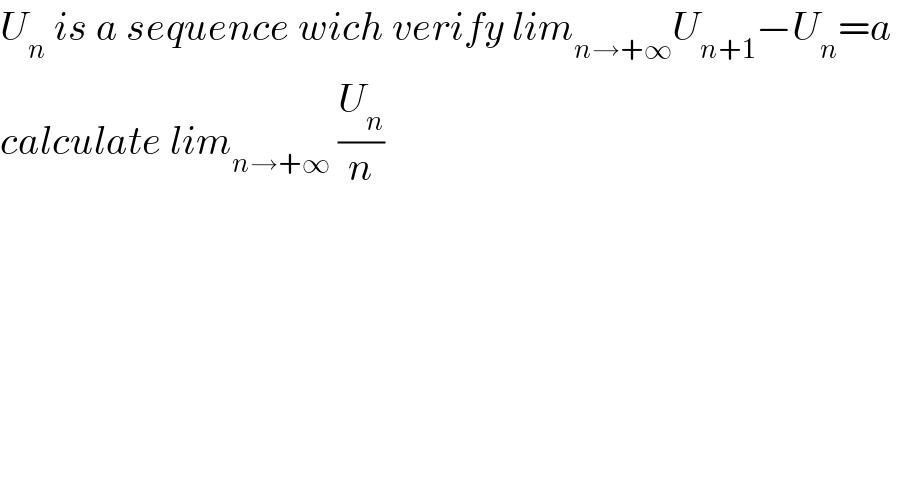
$${U}_{{n}} \:{is}\:{a}\:{sequence}\:{wich}\:{verify}\:{lim}_{{n}\rightarrow+\infty} {U}_{{n}+\mathrm{1}} −{U}_{{n}} ={a}\:\:\: \\ $$$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:\frac{{U}_{{n}} }{{n}} \\ $$
Commented by mathmax by abdo last updated on 20/Jul/19
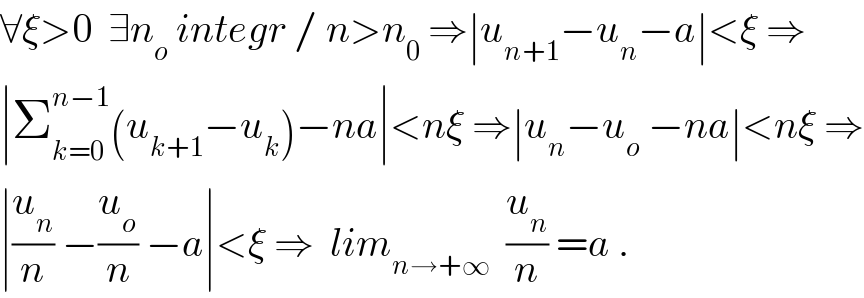
$$\forall\xi>\mathrm{0}\:\:\exists{n}_{{o}} \:{integr}\:/\:{n}>{n}_{\mathrm{0}} \:\Rightarrow\mid{u}_{{n}+\mathrm{1}} −{u}_{{n}} −{a}\mid<\xi\:\Rightarrow \\ $$$$\mid\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({u}_{{k}+\mathrm{1}} −{u}_{{k}} \right)−{na}\mid<{n}\xi\:\Rightarrow\mid{u}_{{n}} −{u}_{{o}} \:−{na}\mid<{n}\xi\:\Rightarrow \\ $$$$\mid\frac{{u}_{{n}} }{{n}}\:−\frac{{u}_{{o}} }{{n}}\:−{a}\mid<\xi\:\Rightarrow\:\:{lim}_{{n}\rightarrow+\infty} \:\:\frac{{u}_{{n}} }{{n}}\:={a}\:. \\ $$
