Question Number 65488 by mathmax by abdo last updated on 30/Jul/19

$${U}_{{n}} {is}\:{a}\:{sequence}\:{wich}\:{verify}\:\:\forall{n}\in{N}^{\bigstar} \\ $$$${U}_{{n}} \:+{U}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{{n}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\:{U}_{{n}} \:{interms}\:{of}\:{n} \\ $$$$\left.\mathrm{2}\right)\:{is}\:{the}\:{sequence}\:{U}_{{n}} {convergent}? \\ $$
Commented by mathmax by abdo last updated on 31/Jul/19
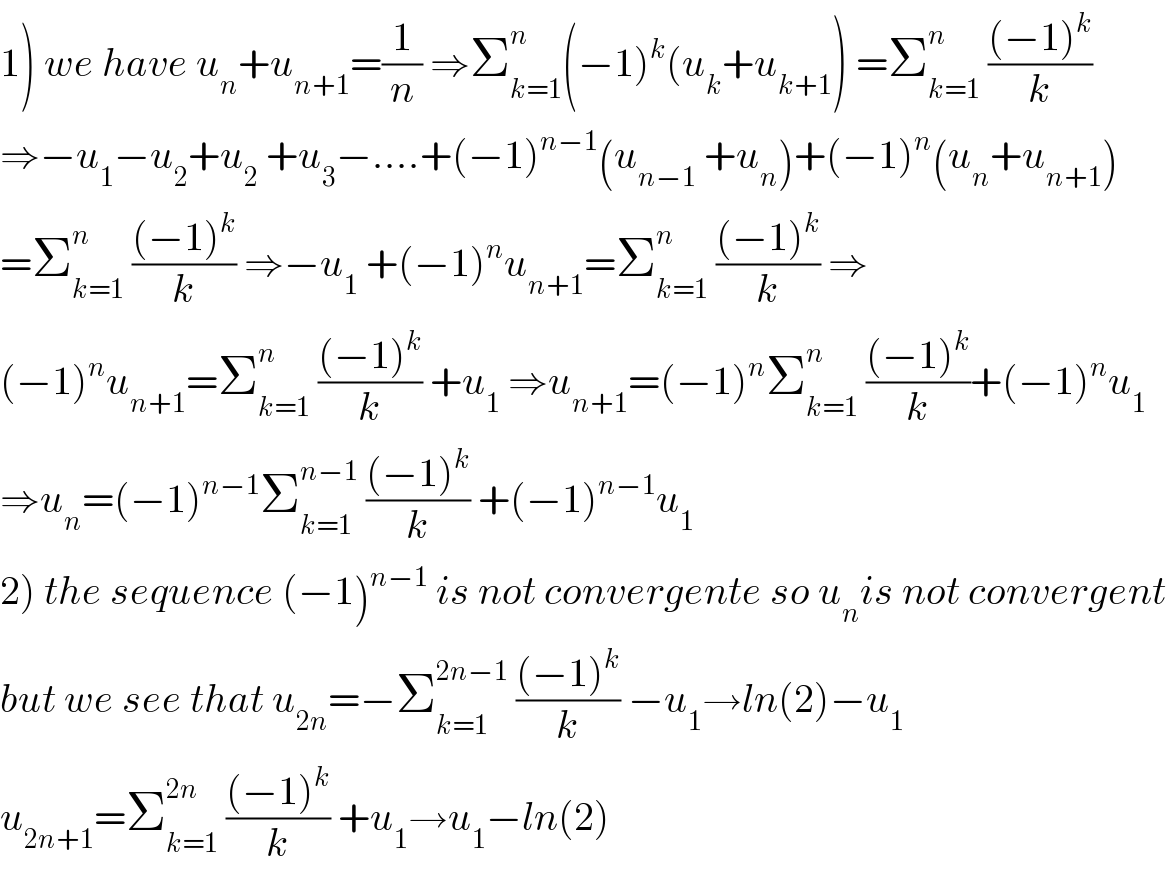
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{u}_{{n}} +{u}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{{n}}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} \left({u}_{{k}} +{u}_{{k}+\mathrm{1}} \right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$$\Rightarrow−{u}_{\mathrm{1}} −{u}_{\mathrm{2}} +{u}_{\mathrm{2}} \:+{u}_{\mathrm{3}} −….+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({u}_{{n}−\mathrm{1}} \:+{u}_{{n}} \right)+\left(−\mathrm{1}\right)^{{n}} \left({u}_{{n}} +{u}_{{n}+\mathrm{1}} \right) \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:\Rightarrow−{u}_{\mathrm{1}} \:+\left(−\mathrm{1}\right)^{{n}} {u}_{{n}+\mathrm{1}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:\Rightarrow \\ $$$$\left(−\mathrm{1}\right)^{{n}} {u}_{{n}+\mathrm{1}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:+{u}_{\mathrm{1}} \:\Rightarrow{u}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}} \sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}+\left(−\mathrm{1}\right)^{{n}} {u}_{\mathrm{1}} \\ $$$$\Rightarrow{u}_{{n}} =\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {u}_{\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{the}\:{sequence}\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{is}\:{not}\:{convergente}\:{so}\:{u}_{{n}} {is}\:{not}\:{convergent} \\ $$$${but}\:{we}\:{see}\:{that}\:{u}_{\mathrm{2}{n}} =−\sum_{{k}=\mathrm{1}} ^{\mathrm{2}{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:−{u}_{\mathrm{1}} \rightarrow{ln}\left(\mathrm{2}\right)−{u}_{\mathrm{1}} \\ $$$${u}_{\mathrm{2}{n}+\mathrm{1}} =\sum_{{k}=\mathrm{1}} ^{\mathrm{2}{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:+{u}_{\mathrm{1}} \rightarrow{u}_{\mathrm{1}} −{ln}\left(\mathrm{2}\right) \\ $$
