Question Number 126552 by mathocean1 last updated on 21/Dec/20
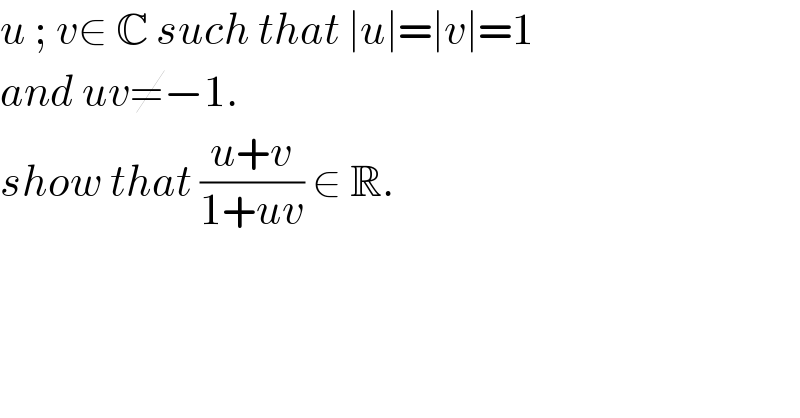
$${u}\:;\:{v}\in\:\mathbb{C}\:{such}\:{that}\:\mid{u}\mid=\mid{v}\mid=\mathrm{1} \\ $$$${and}\:{uv}\neq−\mathrm{1}. \\ $$$${show}\:{that}\:\frac{{u}+{v}}{\mathrm{1}+{uv}}\:\in\:\mathbb{R}. \\ $$
Answered by Olaf last updated on 21/Dec/20
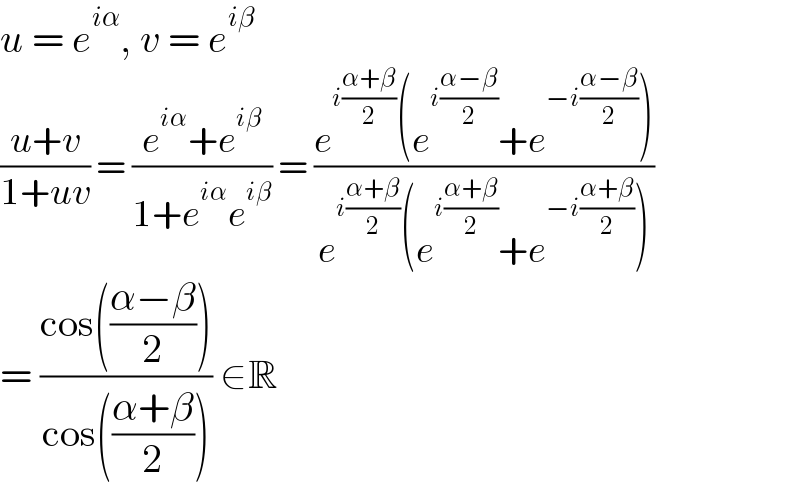
$${u}\:=\:{e}^{{i}\alpha} ,\:{v}\:=\:{e}^{{i}\beta} \\ $$$$\frac{{u}+{v}}{\mathrm{1}+{uv}}\:=\:\frac{{e}^{{i}\alpha} +{e}^{{i}\beta} }{\mathrm{1}+{e}^{{i}\alpha} {e}^{{i}\beta} }\:=\:\frac{{e}^{{i}\frac{\alpha+\beta}{\mathrm{2}}} \left({e}^{{i}\frac{\alpha−\beta}{\mathrm{2}}} +{e}^{−{i}\frac{\alpha−\beta}{\mathrm{2}}} \right)}{{e}^{{i}\frac{\alpha+\beta}{\mathrm{2}}} \left({e}^{{i}\frac{\alpha+\beta}{\mathrm{2}}} +{e}^{−{i}\frac{\alpha+\beta}{\mathrm{2}}} \right)} \\ $$$$=\:\frac{\mathrm{cos}\left(\frac{\alpha−\beta}{\mathrm{2}}\right)}{\mathrm{cos}\left(\frac{\alpha+\beta}{\mathrm{2}}\right)}\:\in\mathbb{R} \\ $$
