Question Number 34724 by mondodotto@gmail.com last updated on 10/May/18
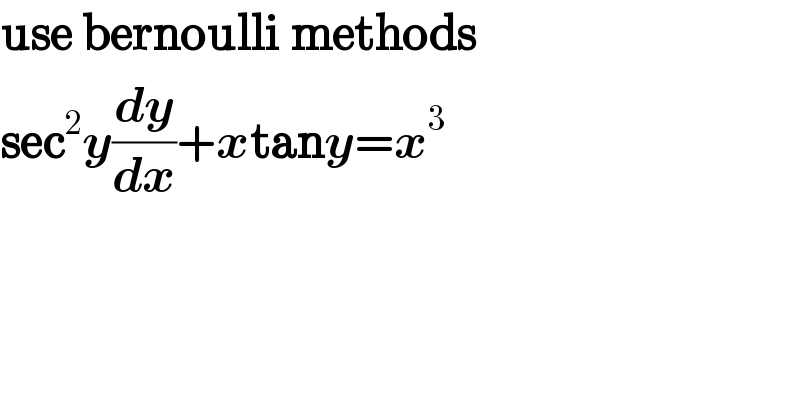
$$\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{bernoulli}}\:\boldsymbol{\mathrm{methods}} \\ $$$$\boldsymbol{\mathrm{sec}}^{\mathrm{2}} \boldsymbol{{y}}\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}+\boldsymbol{{x}\mathrm{tan}{y}}=\boldsymbol{{x}}^{\mathrm{3}} \\ $$
Commented by mondodotto@gmail.com last updated on 10/May/18
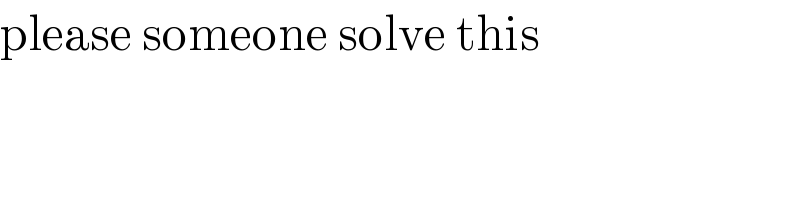
$$\mathrm{please}\:\mathrm{someone}\:\mathrm{solve}\:\mathrm{this}\: \\ $$
Answered by candre last updated on 10/May/18
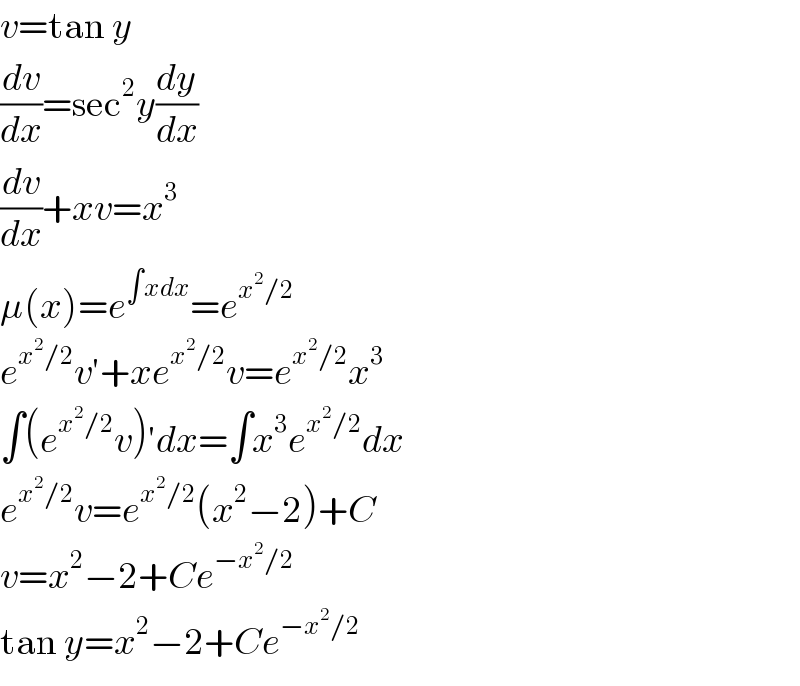
$${v}=\mathrm{tan}\:{y} \\ $$$$\frac{{dv}}{{dx}}=\mathrm{sec}^{\mathrm{2}} {y}\frac{{dy}}{{dx}} \\ $$$$\frac{{dv}}{{dx}}+{xv}={x}^{\mathrm{3}} \\ $$$$\mu\left({x}\right)={e}^{\int{xdx}} ={e}^{{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$${e}^{{x}^{\mathrm{2}} /\mathrm{2}} {v}'+{xe}^{{x}^{\mathrm{2}} /\mathrm{2}} {v}={e}^{{x}^{\mathrm{2}} /\mathrm{2}} {x}^{\mathrm{3}} \\ $$$$\int\left({e}^{{x}^{\mathrm{2}} /\mathrm{2}} {v}\right)'{dx}=\int{x}^{\mathrm{3}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} {dx} \\ $$$${e}^{{x}^{\mathrm{2}} /\mathrm{2}} {v}={e}^{{x}^{\mathrm{2}} /\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}\right)+{C} \\ $$$${v}={x}^{\mathrm{2}} −\mathrm{2}+{Ce}^{−{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$$\mathrm{tan}\:{y}={x}^{\mathrm{2}} −\mathrm{2}+{Ce}^{−{x}^{\mathrm{2}} /\mathrm{2}} \\ $$
Commented by candre last updated on 10/May/18
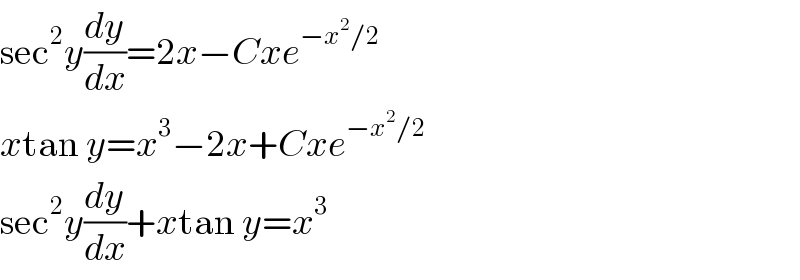
$$\mathrm{sec}^{\mathrm{2}} {y}\frac{{dy}}{{dx}}=\mathrm{2}{x}−{Cxe}^{−{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$${x}\mathrm{tan}\:{y}={x}^{\mathrm{3}} −\mathrm{2}{x}+{Cxe}^{−{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$$\mathrm{sec}^{\mathrm{2}} {y}\frac{{dy}}{{dx}}+{x}\mathrm{tan}\:{y}={x}^{\mathrm{3}} \\ $$
