Question Number 100087 by mathmax by abdo last updated on 24/Jun/20
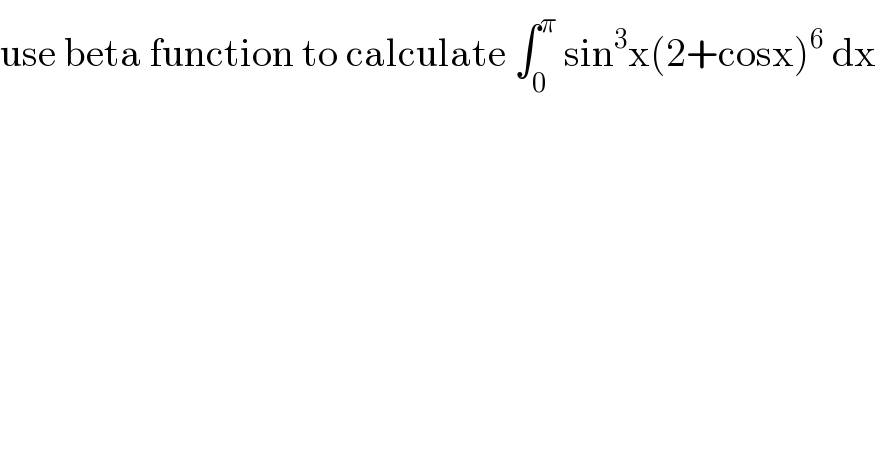
$$\mathrm{use}\:\mathrm{beta}\:\mathrm{function}\:\mathrm{to}\:\mathrm{calculate}\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{sin}^{\mathrm{3}} \mathrm{x}\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{6}} \:\mathrm{dx} \\ $$
Commented by bemath last updated on 25/Jun/20
![∫(cos^2 x−1)(2+cos x)^6 d(cos x) ∫(z^2 −1)(2+z)^6 dz ∫ z^2 (2+z)^6 dz−∫(2+z)^6 dz [(1/7)z^2 (2+z)^7 −(1/(28))z(2+z)^8 +(1/(494))(2+z)^9 −(1/7)(2+z)^7 ]_1 ^(−1) [ (1/7)+(1/(28))+(1/(494))−(1/7)]−[(3^7 /7)−(3^8 /(28))+(3^9 /(494))−(3^7 /7)] = ((3^8 +1)/(28))+((1−3^9 )/(494)) ■](https://www.tinkutara.com/question/Q100128.png)
$$\int\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\left(\mathrm{2}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{6}} \:\mathrm{d}\left(\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\int\left(\mathrm{z}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}+\mathrm{z}\right)^{\mathrm{6}} \:\mathrm{dz}\: \\ $$$$\int\:\mathrm{z}^{\mathrm{2}} \left(\mathrm{2}+\mathrm{z}\right)^{\mathrm{6}} \:\mathrm{dz}−\int\left(\mathrm{2}+\mathrm{z}\right)^{\mathrm{6}} \:\mathrm{dz}\: \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{7}}\mathrm{z}^{\mathrm{2}} \left(\mathrm{2}+\mathrm{z}\right)^{\mathrm{7}} −\frac{\mathrm{1}}{\mathrm{28}}\mathrm{z}\left(\mathrm{2}+\mathrm{z}\right)^{\mathrm{8}} +\frac{\mathrm{1}}{\mathrm{494}}\left(\mathrm{2}+\mathrm{z}\right)^{\mathrm{9}} −\frac{\mathrm{1}}{\mathrm{7}}\left(\mathrm{2}+\mathrm{z}\right)^{\mathrm{7}} \right]_{\mathrm{1}} ^{−\mathrm{1}} \\ $$$$\left[\:\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{28}}+\frac{\mathrm{1}}{\mathrm{494}}−\frac{\mathrm{1}}{\mathrm{7}}\right]−\left[\frac{\mathrm{3}^{\mathrm{7}} }{\mathrm{7}}−\frac{\mathrm{3}^{\mathrm{8}} }{\mathrm{28}}+\frac{\mathrm{3}^{\mathrm{9}} }{\mathrm{494}}−\frac{\mathrm{3}^{\mathrm{7}} }{\mathrm{7}}\right] \\ $$$$=\:\frac{\mathrm{3}^{\mathrm{8}} +\mathrm{1}}{\mathrm{28}}+\frac{\mathrm{1}−\mathrm{3}^{\mathrm{9}} }{\mathrm{494}}\:\blacksquare\: \\ $$$$ \\ $$
Answered by 1549442205 last updated on 26/Jun/20
![F=−∫_0 ^π (1−cos^2 x)(2+cos x)^6 dcos x =_(t=cos x ) ∫(t^2 −1)(t+2)^6 dt=∫[t^2 (t+2)^6 ]d∫t−∫(t+2)^6 dt=A−B A=∫t^2 (t^6 +12t^5 +60t^4 +160t^3 +240t^2 +192t+64)dt =(t^9 /9)+((12t^8 )/8)+((60t^7 )/7)+((160t^6 )/6)+((240t^5 )/5)+((192t^4 )/4)+((64t^3 )/3) B=(t^7 /7)+((12t^6 )/6)+((60t^5 )/5)+((160t^4 )/4)+((240t^3 )/3)+((192t^2 )/2)+64t Hence,∫_0 ^π sin^3 x(2+cos x)^6 dx=(A−B)∣_1 ^(−1) =((t^9 /9)+((12t^8 )/8)+((59t^7 )/7)+((148t^6 )/6)+((180t^5 )/5)+((32t^4 )/4)−((176t^3 )/3)−((192t^2 )/2)−64t)∣_1 ^(−1) =((2053)/(126))−(−((17635)/(126)))=((19688)/(126))=((9844)/(63))≈156.25 The second way: F=∫_0 ^π sin^3 x(2+cos x)^6 dx=∫_0 ^π sin^3 x(cos^6 x+12cos^5 x+60cos^4 x+160cos^3 x+240cos^2 x+192cos x+64)dx Since,∫_0 ^π sin^(2m+1) xcos^(2n+1) xdx= =∫_0 ^(π/2) sin^(2m+1) xcos^(2n+1) xdx+∫_(π/2) ^π sin^(2m+1) x.cos^(2n+1) xdx =_(x=t+(π/2) ) ∫_0 ^(π/2) sin^(2m+1) x.cos^(2n+1) xdx−∫_0 ^(π/2) cos^(2m+1) t.sin^(2n+1) tdt (1/2)B(m+1,n+1)−(1/2)B(n+1,m+1)=0(due to the property of Beta function:B(p,q)=B(q,p) and ,∫_0 ^π sin^(2m) xcos^(2n+1) xdx= =∫_0 ^(π/2) sin^(2m) xcos^(2n+1) xdx+∫_(π/2) ^π sin^(2m) x.cos^(2n+1) xdx ==∫_0 ^(π/2) sin^(2m) xcos^(2n+1) xdx+∫_0 ^(π/2) cos^(2m) x.sin^(2n+1) xdx= (1/2)B(((2m+1)/2),n+1)+(1/2)B(n+1,((2m+1)/2))=B(((2m+1)/2),n+1),so F=∫_0 ^π sin^3 x(cos^6 x+12cos^5 x+60cos^4 x+160cos^3 x+240cos^2 x+192cos x+64)dx =B(2,(7/2))+60B(2,(5/2))+240B(2,(3/2))+64B(2,(1/2)) B(p,q)=((Γ(p).Γ(q))/(Γ(p+q))),so B(2,(7/2))=((Γ(2).Γ((7/2)))/(Γ(2+(7/2)))) Γ(2)=1,Γ((1/2))=(√π),Γ((3/2))=((√π)/2),Γ((5/2))=((3(√π))/4),Γ((7/2))=((15(√π))/8) ⇒Γ(2+(7/2))=Γ(5+(1/2))=((3.5.7.9)/2^5 )(√π)=((945(√π))/(32)) ⇒B(2,(7/2))=((1.((15(√π))/8))/((945(√π))/(32)))=((12)/(189))=(4/(63)) B(2,(5/2))=((Γ(2).Γ((5/2)))/(Γ(2+(5/2))))=((1.((3(√π))/4))/(Γ(4+(1/2))))=(((3(√π))/4)/((3.5.7(√π))/(16)))=(4/(35)) B(2,(3/2))=((Γ(2).Γ((3/2)))/(Γ(2+(3/2))))=(((√π)/2)/(Γ(3+(1/2))))=(((√π)/2)/((3.5(√π))/8))=(4/(15)) B(2,(1/2))=((Γ(2).Γ((1/2)))/(Γ(2+(1/2))))=((√π)/((3(√π))/4))=(4/3). Therefore,F=(4/(63))+60.(4/(35))+240.(4/(15))+64.(4/3) =((9844)/(63))](https://www.tinkutara.com/question/Q100127.png)
$$\mathrm{F}=−\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{2}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{6}} \mathrm{dcos}\:\mathrm{x} \\ $$$$\underset{\mathrm{t}=\mathrm{cos}\:\mathrm{x}\:\:} {=}\:\:\int\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{6}} \mathrm{dt}=\int\left[\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{6}} \right]\mathrm{d}\int\mathrm{t}−\int\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{6}} \mathrm{dt}=\mathrm{A}−\mathrm{B} \\ $$$$\mathrm{A}=\int\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{6}} +\mathrm{12t}^{\mathrm{5}} +\mathrm{60t}^{\mathrm{4}} +\mathrm{160t}^{\mathrm{3}} +\mathrm{240t}^{\mathrm{2}} +\mathrm{192t}+\mathrm{64}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{t}^{\mathrm{9}} }{\mathrm{9}}+\frac{\mathrm{12t}^{\mathrm{8}} }{\mathrm{8}}+\frac{\mathrm{60t}^{\mathrm{7}} }{\mathrm{7}}+\frac{\mathrm{160t}^{\mathrm{6}} }{\mathrm{6}}+\frac{\mathrm{240t}^{\mathrm{5}} }{\mathrm{5}}+\frac{\mathrm{192t}^{\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{64t}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\mathrm{B}=\frac{\mathrm{t}^{\mathrm{7}} }{\mathrm{7}}+\frac{\mathrm{12t}^{\mathrm{6}} }{\mathrm{6}}+\frac{\mathrm{60t}^{\mathrm{5}} }{\mathrm{5}}+\frac{\mathrm{160t}^{\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{240t}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{192t}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{64t} \\ $$$$\mathrm{Hence},\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{3}} \mathrm{x}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{6}} \mathrm{dx}=\left(\mathrm{A}−\mathrm{B}\right)\mid_{\mathrm{1}} ^{−\mathrm{1}} \\ $$$$=\left(\frac{\mathrm{t}^{\mathrm{9}} }{\mathrm{9}}+\frac{\mathrm{12t}^{\mathrm{8}} }{\mathrm{8}}+\frac{\mathrm{59t}^{\mathrm{7}} }{\mathrm{7}}+\frac{\mathrm{148t}^{\mathrm{6}} }{\mathrm{6}}+\frac{\mathrm{180t}^{\mathrm{5}} }{\mathrm{5}}+\frac{\mathrm{32t}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{176t}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{192t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{64t}\right)\mid_{\mathrm{1}} ^{−\mathrm{1}} \\ $$$$=\frac{\mathrm{2053}}{\mathrm{126}}−\left(−\frac{\mathrm{17635}}{\mathrm{126}}\right)=\frac{\mathrm{19688}}{\mathrm{126}}=\frac{\mathrm{9844}}{\mathrm{63}}\approx\mathrm{156}.\mathrm{25} \\ $$$$\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{second}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\mathrm{F}=\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{3}} \mathrm{x}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{6}} \mathrm{dx}=\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{3}} \mathrm{x}\left(\mathrm{cos}^{\mathrm{6}} \mathrm{x}+\mathrm{12cos}^{\mathrm{5}} \mathrm{x}+\mathrm{60cos}^{\mathrm{4}} \mathrm{x}+\mathrm{160cos}^{\mathrm{3}} \mathrm{x}+\mathrm{240cos}^{\mathrm{2}} \mathrm{x}+\mathrm{192cos}\:\mathrm{x}+\mathrm{64}\right)\mathrm{dx} \\ $$$$\mathrm{Since},\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{2m}+\mathrm{1}} \mathrm{xcos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}= \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2m}+\mathrm{1}} \mathrm{xcos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{sin}^{\mathrm{2m}+\mathrm{1}} \mathrm{x}.\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx} \\ $$$$\underset{\mathrm{x}=\mathrm{t}+\frac{\pi}{\mathrm{2}}\:\:\:} {=}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2m}+\mathrm{1}} \mathrm{x}.\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2m}+\mathrm{1}} \mathrm{t}.\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \mathrm{tdt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\mathrm{m}+\mathrm{1},\mathrm{n}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\mathrm{n}+\mathrm{1},\mathrm{m}+\mathrm{1}\right)=\mathrm{0}\left(\mathrm{due}\:\mathrm{to}\:\right. \\ $$$$\mathrm{the}\:\mathrm{property}\:\mathrm{of}\:\mathrm{Beta}\:\mathrm{function}:\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)=\mathrm{B}\left(\mathrm{q},\mathrm{p}\right) \\ $$$$\mathrm{and}\:,\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{2m}} \mathrm{xcos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}= \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2m}} \mathrm{xcos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{sin}^{\mathrm{2m}} \mathrm{x}.\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx} \\ $$$$==\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2m}} \mathrm{xcos}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2m}} \mathrm{x}.\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\frac{\mathrm{2m}+\mathrm{1}}{\mathrm{2}},\mathrm{n}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{B}\left(\mathrm{n}+\mathrm{1},\frac{\mathrm{2m}+\mathrm{1}}{\mathrm{2}}\right)=\mathrm{B}\left(\frac{\mathrm{2m}+\mathrm{1}}{\mathrm{2}},\mathrm{n}+\mathrm{1}\right),\mathrm{so} \\ $$$$\mathrm{F}=\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{3}} \mathrm{x}\left(\mathrm{cos}^{\mathrm{6}} \mathrm{x}+\mathrm{12cos}^{\mathrm{5}} \mathrm{x}+\mathrm{60cos}^{\mathrm{4}} \mathrm{x}+\mathrm{160cos}^{\mathrm{3}} \mathrm{x}+\mathrm{240cos}^{\mathrm{2}} \mathrm{x}+\mathrm{192cos}\:\mathrm{x}+\mathrm{64}\right)\mathrm{dx} \\ $$$$=\mathrm{B}\left(\mathrm{2},\frac{\mathrm{7}}{\mathrm{2}}\right)+\mathrm{60B}\left(\mathrm{2},\frac{\mathrm{5}}{\mathrm{2}}\right)+\mathrm{240B}\left(\mathrm{2},\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{64B}\left(\mathrm{2},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)=\frac{\Gamma\left(\mathrm{p}\right).\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)},\mathrm{so}\:\mathrm{B}\left(\mathrm{2},\frac{\mathrm{7}}{\mathrm{2}}\right)=\frac{\Gamma\left(\mathrm{2}\right).\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}+\frac{\mathrm{7}}{\mathrm{2}}\right)} \\ $$$$\Gamma\left(\mathrm{2}\right)=\mathrm{1},\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi},\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}},\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}},\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)=\frac{\mathrm{15}\sqrt{\pi}}{\mathrm{8}} \\ $$$$\Rightarrow\Gamma\left(\mathrm{2}+\frac{\mathrm{7}}{\mathrm{2}}\right)=\Gamma\left(\mathrm{5}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}.\mathrm{9}}{\mathrm{2}^{\mathrm{5}} }\sqrt{\pi}=\frac{\mathrm{945}\sqrt{\pi}}{\mathrm{32}} \\ $$$$\Rightarrow\mathrm{B}\left(\mathrm{2},\frac{\mathrm{7}}{\mathrm{2}}\right)=\frac{\mathrm{1}.\frac{\mathrm{15}\sqrt{\pi}}{\mathrm{8}}}{\frac{\mathrm{945}\sqrt{\pi}}{\mathrm{32}}}=\frac{\mathrm{12}}{\mathrm{189}}=\frac{\mathrm{4}}{\mathrm{63}} \\ $$$$\mathrm{B}\left(\mathrm{2},\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\Gamma\left(\mathrm{2}\right).\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}+\frac{\mathrm{5}}{\mathrm{2}}\right)}=\frac{\mathrm{1}.\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}}{\Gamma\left(\mathrm{4}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}}{\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}\sqrt{\pi}}{\mathrm{16}}}=\frac{\mathrm{4}}{\mathrm{35}} \\ $$$$\mathrm{B}\left(\mathrm{2},\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\Gamma\left(\mathrm{2}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}}\right)}=\frac{\frac{\sqrt{\pi}}{\mathrm{2}}}{\Gamma\left(\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\frac{\sqrt{\pi}}{\mathrm{2}}}{\frac{\mathrm{3}.\mathrm{5}\sqrt{\pi}}{\mathrm{8}}}=\frac{\mathrm{4}}{\mathrm{15}} \\ $$$$\mathrm{B}\left(\mathrm{2},\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\Gamma\left(\mathrm{2}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\sqrt{\pi}}{\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}}=\frac{\mathrm{4}}{\mathrm{3}}. \\ $$$$\mathrm{Therefore},\mathrm{F}=\frac{\mathrm{4}}{\mathrm{63}}+\mathrm{60}.\frac{\mathrm{4}}{\mathrm{35}}+\mathrm{240}.\frac{\mathrm{4}}{\mathrm{15}}+\mathrm{64}.\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{9844}}{\mathrm{63}} \\ $$
Commented by mathmax by abdo last updated on 25/Jun/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{this}\:\mathrm{hardwork}.. \\ $$
