Using-approach-prove-that-lim-z-i-3z-4-2z-3-8z-2-2z-5-z-i-4-4i-Help-

Question Number 185243 by Mastermind last updated on 19/Jan/23

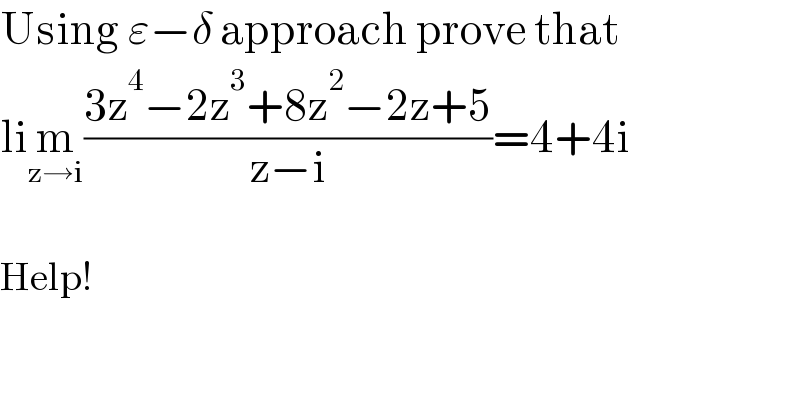
Using ε−δ approach prove that lim_(z→i) ((3z^4 −2z^3 +8z^2 −2z+5)/(z−i))=4+4i Help!

$$\mathrm{Using}\:\varepsilon−\delta\:\mathrm{approach}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{li}\underset{\mathrm{z}\rightarrow\mathrm{i}} {\mathrm{m}}\frac{\mathrm{3z}^{\mathrm{4}} −\mathrm{2z}^{\mathrm{3}} +\mathrm{8z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{5}}{\mathrm{z}−\mathrm{i}}=\mathrm{4}+\mathrm{4i} \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Commented by Frix last updated on 19/Jan/23

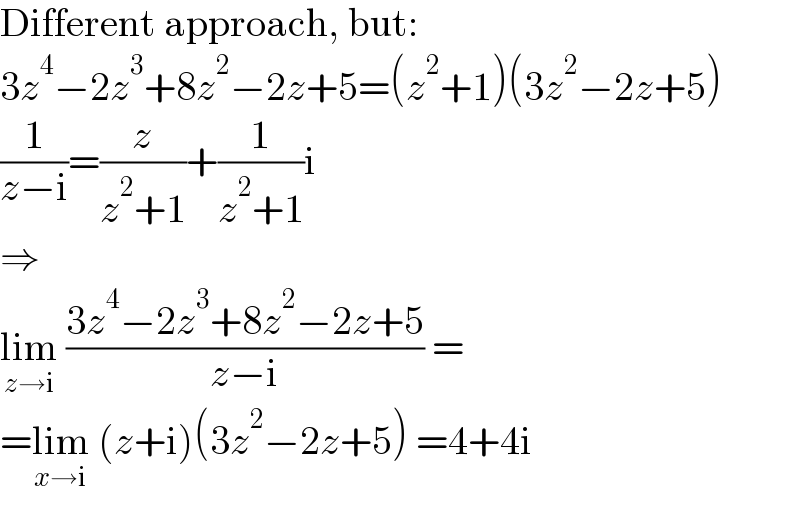
Different approach, but: 3z^4 −2z^3 +8z^2 −2z+5=(z^2 +1)(3z^2 −2z+5) (1/(z−i))=(z/(z^2 +1))+(1/(z^2 +1))i ⇒ lim_(z→i) ((3z^4 −2z^3 +8z^2 −2z+5)/(z−i)) = =lim_(x→i) (z+i)(3z^2 −2z+5) =4+4i

$$\mathrm{Different}\:\mathrm{approach},\:\mathrm{but}: \\ $$$$\mathrm{3}{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{3}} +\mathrm{8}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}=\left({z}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}\right) \\ $$$$\frac{\mathrm{1}}{{z}−\mathrm{i}}=\frac{{z}}{{z}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{{z}^{\mathrm{2}} +\mathrm{1}}\mathrm{i} \\ $$$$\Rightarrow \\ $$$$\underset{{z}\rightarrow\mathrm{i}} {\mathrm{lim}}\:\frac{\mathrm{3}{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{3}} +\mathrm{8}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}}{{z}−\mathrm{i}}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{i}} {\mathrm{lim}}\:\left({z}+\mathrm{i}\right)\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}\right)\:=\mathrm{4}+\mathrm{4i} \\ $$

Commented by Mastermind last updated on 19/Jan/23

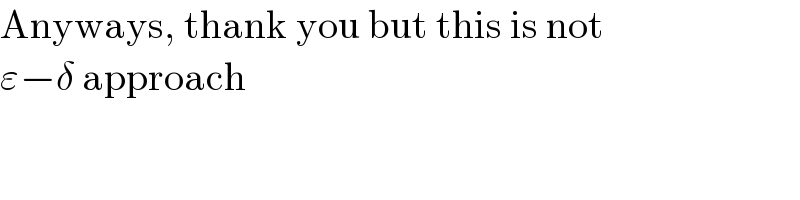
Anyways, thank you but this is not ε−δ approach

$$\mathrm{Anyways},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not} \\ $$$$\varepsilon−\delta\:\mathrm{approach}\: \\ $$

Commented by Frix last updated on 19/Jan/23

I know. Since I′m not The Omniscient Answering Machine (if I were the answer would have been 42 of course) I simply don′t know the ε−δ approach. You tell me please.

$$\mathrm{I}\:\mathrm{know}. \\ $$$$\mathrm{Since}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{The}\:\mathrm{Omniscient}\:\mathrm{Answering} \\ $$$$\mathrm{Machine}\:\left(\mathrm{if}\:\mathrm{I}\:\mathrm{were}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{would}\:\mathrm{have}\right. \\ $$$$\left.\mathrm{been}\:\mathrm{42}\:\mathrm{of}\:\mathrm{course}\right)\:\mathrm{I}\:\mathrm{simply}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the} \\ $$$$\epsilon−\delta\:\mathrm{approach}.\:\mathrm{You}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{please}. \\ $$

Answered by 123564 last updated on 19/Jan/23

Commented by Mastermind last updated on 20/Jan/23

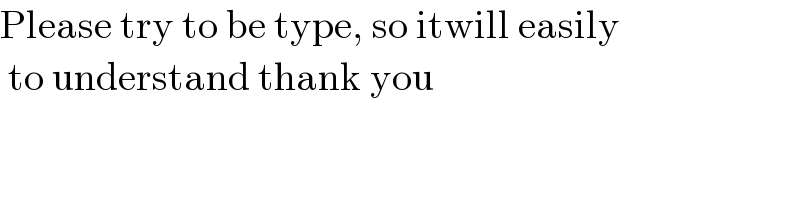
Please try to be type, so itwill easily to understand thank you

$$\mathrm{Please}\:\mathrm{try}\:\mathrm{to}\:\mathrm{be}\:\mathrm{type},\:\mathrm{so}\:\mathrm{itwill}\:\mathrm{easily} \\ $$$$\:\mathrm{to}\:\mathrm{understand}\:\mathrm{thank}\:\mathrm{you} \\ $$

Facebook Tweet Pin

Using-approach-prove-that-lim-z-i-3z-4-2z-3-8z-2-2z-5-z-i-4-4i-Help-

Leave a Reply Cancel reply