Question Number 169706 by MikeH last updated on 06/May/22
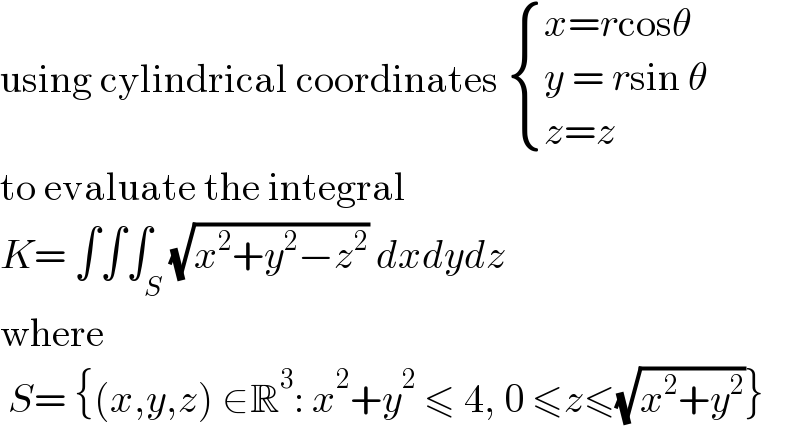
$$\mathrm{using}\:\mathrm{cylindrical}\:\mathrm{coordinates}\:\begin{cases}{{x}={r}\mathrm{cos}\theta}\\{{y}\:=\:{r}\mathrm{sin}\:\theta}\\{{z}={z}}\end{cases} \\ $$$$\mathrm{to}\:\mathrm{evaluate}\:\mathrm{the}\:\mathrm{integral} \\ $$$${K}=\:\int\int\int_{{S}} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{z}^{\mathrm{2}} }\:{dxdydz} \\ $$$$\mathrm{where} \\ $$$$\:{S}=\:\left\{\left({x},{y},{z}\right)\:\in\mathbb{R}^{\mathrm{3}} :\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\leqslant\:\mathrm{4},\:\mathrm{0}\:\leqslant{z}\leqslant\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right\} \\ $$
