using-taylors-expansion-find-find-the-value-of-a-tan45-1-b-sin30-1-

Question Number 46534 by peter frank last updated on 28/Oct/18

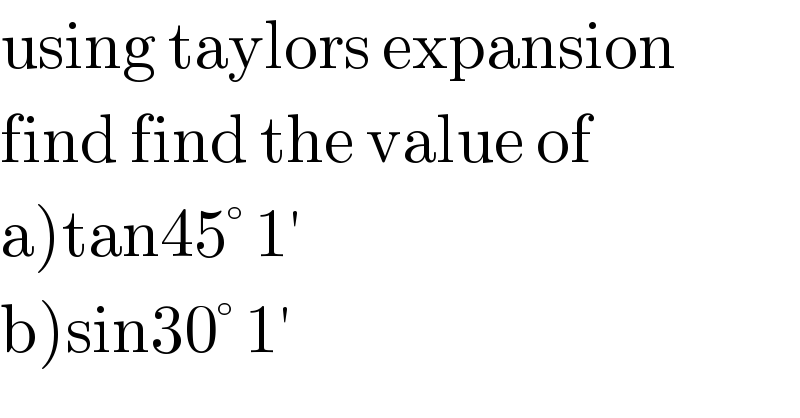
using taylors expansion

find find the value of

a) \tan 45 ° 1^{'}

b) \sin 30 ° 1^{'}

Answered by tanmay.chaudhury50@gmail.com last updated on 28/Oct/18

a) y = f (x) w h e n x c h a n g e s t o x + △ x

y c h a n g e s t o y + △ y

h e r e f (x) = t a n x

y = t a n x \frac{d y}{d x} = {s e c}^{2} x

\frac{d y}{d x} = \frac{△ y}{△ x}

△ y = \frac{d y}{d x} △ x

△ y = {s e c}^{2} x . △ x

△ x = 1^{^{'}} = {(\frac{1}{60})}^{o} = \frac{π}{180} \times \frac{1}{60} = 0.00029

△ y = {s e c}^{2} 45^{o} \times 0.00029 = 0.00058

s o v a l u e o f t a n (45^{o} 1^{'}) = 1 + 0.00058 = 1.00058

b) △ y = \frac{d y}{d x} △ x

y = s i n x \frac{d y}{d x} = c o s x

△ y = c o s x . △ x

△ y = c o s 30^{o} \times 0.00029 = \frac{\sqrt{3}}{2} \times 0.00029 = 0.00025

s o s i n (30^{o} 1^{'}) = 0.5 + 0.00025 = 0.50025