Question Number 84263 by Rio Michael last updated on 10/Mar/20
![Using the approximation h((dy/dx))_n ≈ y_(n+1) −y_n and that (dy/dx) = 1, y =2 when x = 0 . then , y_1 = [A] h−2 [B] h + 2 [C] h−1 [D] h + 1](https://www.tinkutara.com/question/Q84263.png)
$$\mathrm{Using}\:\mathrm{the}\:\mathrm{approximation} \\ $$$$\:{h}\left(\frac{{dy}}{{dx}}\right)_{{n}} \:\approx\:{y}_{{n}+\mathrm{1}} −{y}_{{n}} \:\mathrm{and}\:\mathrm{that}\:\frac{{dy}}{{dx}}\:=\:\mathrm{1},\:{y}\:=\mathrm{2} \\ $$$$\mathrm{when}\:{x}\:=\:\mathrm{0}\:.\:\mathrm{then}\:,\:{y}_{\mathrm{1}} \:= \\ $$$$\left[\mathrm{A}\right]\:{h}−\mathrm{2} \\ $$$$\left[\mathrm{B}\right]\:{h}\:+\:\mathrm{2} \\ $$$$\left[\mathrm{C}\right]\:{h}−\mathrm{1} \\ $$$$\left[\mathrm{D}\right]\:{h}\:+\:\mathrm{1} \\ $$
Answered by mind is power last updated on 11/Mar/20
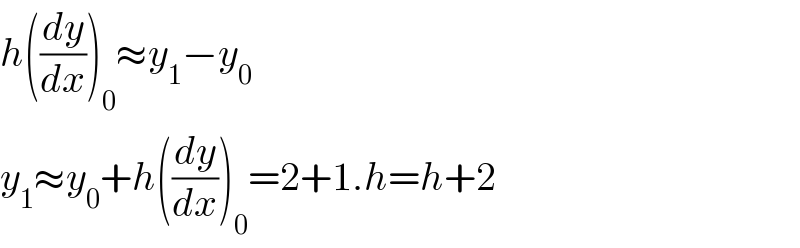
$${h}\left(\frac{{dy}}{{dx}}\right)_{\mathrm{0}} \approx{y}_{\mathrm{1}} −{y}_{\mathrm{0}} \\ $$$${y}_{\mathrm{1}} \approx{y}_{\mathrm{0}} +{h}\left(\frac{{dy}}{{dx}}\right)_{\mathrm{0}} =\mathrm{2}+\mathrm{1}.{h}={h}+\mathrm{2} \\ $$
Commented by Rio Michael last updated on 11/Mar/20

$$\mathrm{thanks} \\ $$
