Question Number 112059 by Aina Samuel Temidayo last updated on 05/Sep/20
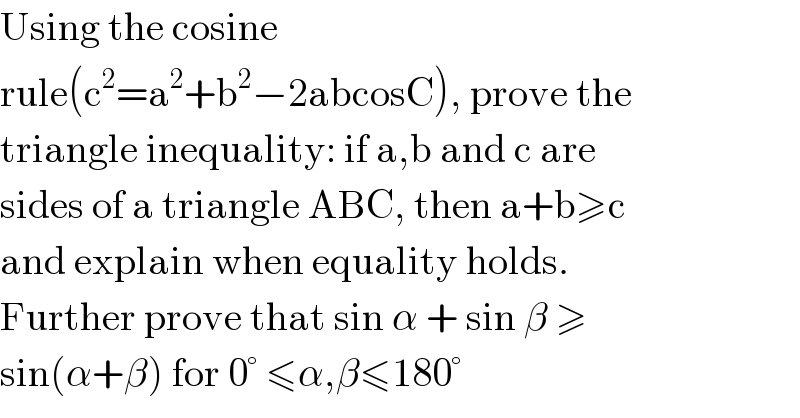
Answered by 1549442205PVT last updated on 06/Sep/20

Commented by Aina Samuel Temidayo last updated on 06/Sep/20

Commented by Aina Samuel Temidayo last updated on 06/Sep/20

Commented by 1549442205PVT last updated on 06/Sep/20

Commented by Aina Samuel Temidayo last updated on 06/Sep/20

Commented by Aina Samuel Temidayo last updated on 06/Sep/20

