Question Number 36433 by prof Abdo imad last updated on 02/Jun/18
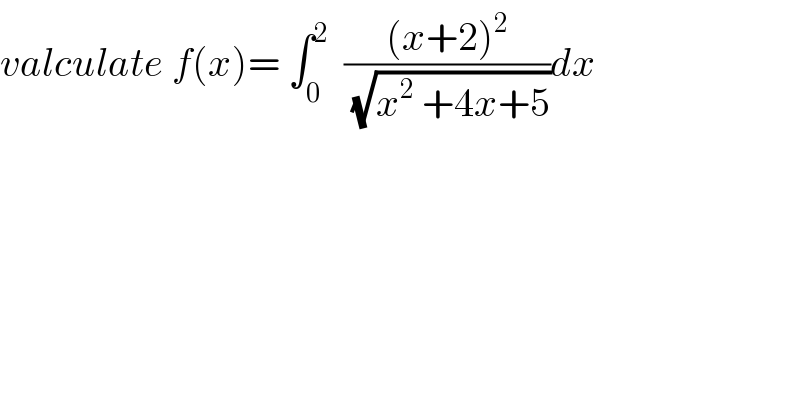
$${valculate}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}{x}+\mathrm{5}}}{dx} \\ $$
Commented by abdo.msup.com last updated on 02/Jun/18
![we have I = ∫_0 ^2 ((x^2 +4x +4)/( (√(x^2 +4x+5))))dx =∫_0 ^2 ((x^2 +4x +5 −1)/( (√(x^2 +4x +5))))dx = ∫_0 ^2 (√(x^2 +4x +5))dx − ∫_0 ^2 (dx/( (√(x^2 +4x +5)))) = I_1 −I_2 I_1 = ∫_0 ^2 (√((x+2)^2 +1))dx =_(x+2=sh(t)) ∫_(argsh(2)) ^(argsh(4)) cht cht dt =∫_(ln( 2 +(√5))) ^(ln(4 +(√(17)))) ((1+ch(2x))/2)dx =(1/2)ln{((4+(√(17)))/(2+(√5)))} +(1/4)[sh(2x)]_(ln(2+(√5))) ^(ln(4 +(√(17)))) =(1/2)ln{((4 +(√(17)))/(2+(√5)))} +(1/4){ (((4+(√(17)))^2 −(2+(√5))^2 )/2)} I_2 = ∫_0 ^2 (dx/( (√(x^2 +4x +4)))) = ∫_0 ^2 (dx/( (√((x+2)^2 +1)))) =_(x+2 =sh(t)) ∫_(ln(2+(√5))) ^(ln(4 +(√(17)))) ((cht dt)/(ch(t))) = ln( ((4 +(√(17)))/(2 +(√5)))) so I =−(1/2)ln{((4+(√(17)))/(2+(√5)))} +(1/8){(4+(√(17)))^2 −(2+(√5))^2 }](https://www.tinkutara.com/question/Q36505.png)
$${we}\:{have}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{4}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}{x}+\mathrm{5}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}\:+\mathrm{5}\:−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{5}}}{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{5}}{dx}\:\:−\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{5}}} \\ $$$$=\:{I}_{\mathrm{1}} \:−{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$$=_{{x}+\mathrm{2}={sh}\left({t}\right)} \:\:\:\int_{{argsh}\left(\mathrm{2}\right)} ^{{argsh}\left(\mathrm{4}\right)} \:\:\:{cht}\:{cht}\:{dt} \\ $$$$=\int_{{ln}\left(\:\mathrm{2}\:+\sqrt{\mathrm{5}}\right)} ^{{ln}\left(\mathrm{4}\:+\sqrt{\mathrm{17}}\right)} \:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{x}\right)}{\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\frac{\mathrm{4}+\sqrt{\mathrm{17}}}{\mathrm{2}+\sqrt{\mathrm{5}}}\right\}\:\:\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sh}\left(\mathrm{2}{x}\right)\right]_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} ^{{ln}\left(\mathrm{4}\:+\sqrt{\mathrm{17}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\frac{\mathrm{4}\:+\sqrt{\mathrm{17}}}{\mathrm{2}+\sqrt{\mathrm{5}}}\right\}\:\:+\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\:\frac{\left(\mathrm{4}+\sqrt{\mathrm{17}}\right)^{\mathrm{2}} \:−\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{2}}\right\} \\ $$$${I}_{\mathrm{2}} \:=\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{4}}} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\:\frac{{dx}}{\:\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$$=_{{x}+\mathrm{2}\:={sh}\left({t}\right)} \:\:\int_{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} ^{{ln}\left(\mathrm{4}\:+\sqrt{\mathrm{17}}\right)} \:\:\:\:\frac{{cht}\:{dt}}{{ch}\left({t}\right)} \\ $$$$=\:{ln}\left(\:\frac{\mathrm{4}\:+\sqrt{\mathrm{17}}}{\mathrm{2}\:+\sqrt{\mathrm{5}}}\right)\:{so} \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\frac{\mathrm{4}+\sqrt{\mathrm{17}}}{\mathrm{2}+\sqrt{\mathrm{5}}}\right\}\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\left(\mathrm{4}+\sqrt{\mathrm{17}}\right)^{\mathrm{2}} \:−\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} \right\} \\ $$
Answered by MJS last updated on 02/Jun/18
![∫(((x+2)^2 )/( (√(x^2 +4x+5))))dx=∫((x^2 +4x+4+1−1)/( (√(x^2 +4x+5))))dx= =∫((x^2 +4x+5)/( (√(x^2 +4x+5))))dx−∫(dx/( (√(x^2 +4x+5))))= =∫(√(x^2 +4x+5))dx−∫(dx/( (√(x^2 +4x+5))))o [((∫(√(x^2 +4x+5))dx=∫(√((x+2)^2 +1))dx=)),(( [t=x+2 → dx=dt])),((=∫(√(t^2 +1))dt=)),(( [u=arctan t → dt=sec^2 u du])),((=∫sec^2 u (√(tan^2 u +1))du=)),((=∫sec^3 u du=)),(( [∫sec^n u du=((sec^(n−2) u tan u)/(n−1))+((n−2)/(n−1))∫sec^(n−2) u du])),((=((sec u tan u)/2)+(1/2)∫sec u du=)),((=((sec u tan u)/2)+(1/2)ln(tan u +sec u)=)),((=(1/2)(t(√(t^2 +1))+ln(t+(√(t^2 +1))))=)),((=(1/2)((x+2)(√(x^2 +4x+5))+ln(x+2+(√(x^2 +4x+5)))))) ] [((∫(dx/( (√(x^2 +4x+5))))=∫(dx/( (√((x+2)^2 +1))))=)),(( [t=x+2 → dx=dt])),((=∫(dt/( (√(t^2 +1))))=ln(t+(√(t^2 +1)))=)),((=ln(x+2+(√(x^2 +4x+5))))) ] =(1/2)((x+2)(√(x^2 +4x+5))−ln(x+2+(√(x^2 +4x+5))))+C ∫_0 ^2 (((x+2)^2 )/( (√(x^2 +4x+5))))dx= =2(√(17))−(√5)+(1/2)(ln((√5)+2)−ln((√(17))+4))≈ ≈5.68460](https://www.tinkutara.com/question/Q36498.png)
$$\int\frac{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}{dx}=\int\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}+\mathrm{1}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}{dx}= \\ $$$$=\int\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}{dx}−\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}= \\ $$$$=\int\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}{dx}−\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}{o} \\ $$$$ \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}{dx}=\int\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}{dx}=}\\{\:\:\:\:\:\left[{t}={x}+\mathrm{2}\:\rightarrow\:{dx}={dt}\right]}\\{=\int\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=}\\{\:\:\:\:\:\left[{u}=\mathrm{arctan}\:{t}\:\rightarrow\:{dt}=\mathrm{sec}^{\mathrm{2}} \:{u}\:{du}\right]}\\{=\int\mathrm{sec}^{\mathrm{2}} \:{u}\:\sqrt{\mathrm{tan}^{\mathrm{2}} \:{u}\:+\mathrm{1}}{du}=}\\{=\int\mathrm{sec}^{\mathrm{3}} \:{u}\:{du}=}\\{\:\:\:\:\:\left[\int\mathrm{sec}^{{n}} \:{u}\:{du}=\frac{\mathrm{sec}^{{n}−\mathrm{2}} \:{u}\:\mathrm{tan}\:{u}}{{n}−\mathrm{1}}+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{sec}^{{n}−\mathrm{2}} \:{u}\:{du}\right]}\\{=\frac{\mathrm{sec}\:{u}\:\mathrm{tan}\:{u}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sec}\:{u}\:{du}=}\\{=\frac{\mathrm{sec}\:{u}\:\mathrm{tan}\:{u}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{tan}\:{u}\:+\mathrm{sec}\:{u}\right)=}\\{=\frac{\mathrm{1}}{\mathrm{2}}\left({t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}+\mathrm{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)\right)=}\\{=\frac{\mathrm{1}}{\mathrm{2}}\left(\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}+\mathrm{ln}\left({x}+\mathrm{2}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}\right)\right)}\end{bmatrix} \\ $$$$ \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}=\int\frac{{dx}}{\:\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}}=}\\{\:\:\:\:\:\left[{t}={x}+\mathrm{2}\:\rightarrow\:{dx}={dt}\right]}\\{=\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}=\mathrm{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)=}\\{=\mathrm{ln}\left({x}+\mathrm{2}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}\right)}\end{bmatrix} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}−\mathrm{ln}\left({x}+\mathrm{2}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}\right)\right)+{C} \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\frac{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}{dx}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{17}}−\sqrt{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)−\mathrm{ln}\left(\sqrt{\mathrm{17}}+\mathrm{4}\right)\right)\approx \\ $$$$\approx\mathrm{5}.\mathrm{68460} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18
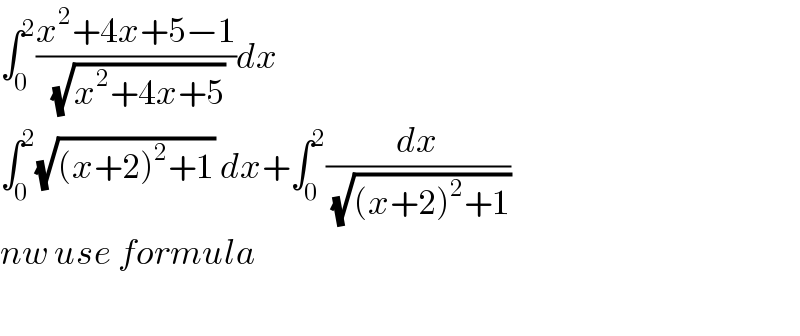
$$\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}\:{dx}+\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{dx}}{\:\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}} \\ $$$${nw}\:{use}\:{formula} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18

Commented by abdo.msup.com last updated on 02/Jun/18
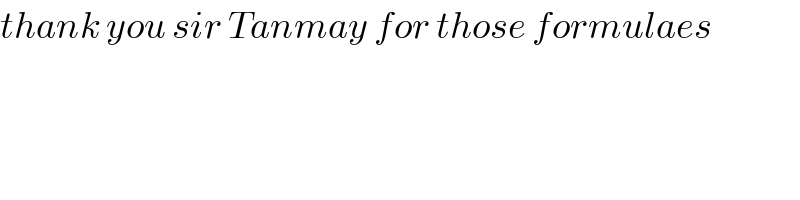
$${thank}\:{you}\:{sir}\:{Tanmay}\:{for}\:{those}\:{formulaes} \\ $$
