Question Number 180689 by SANOGO last updated on 15/Nov/22
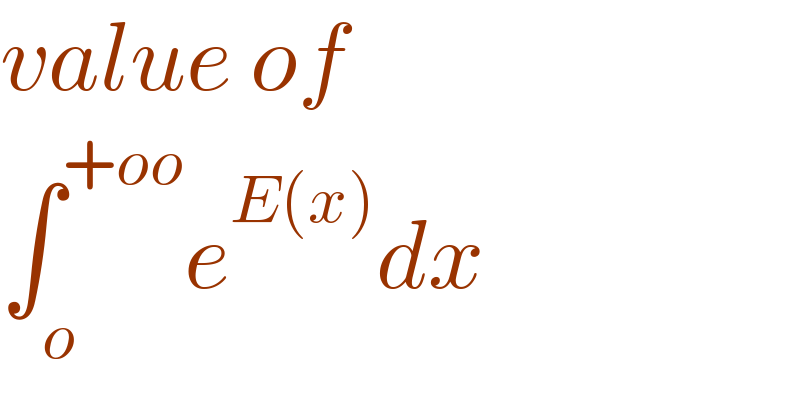
$${value}\:{of}\: \\ $$$$\int_{{o}} ^{+{oo}} {e}^{{E}\left({x}\right)} {dx} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 16/Nov/22
![∫_0 ^∞ e^([x]) dx=Σ_(k=0) ^∞ ∫_k ^(k+1) e^x dx=Σ_(k=0) ^∞ (e^(k+1) −e^k ) =(e−1)+(e^2 −e)+∙∙∙+(e^n −e^(n−1) )+(e^(n+1) −e^n )+... =lim_(n→+∞) (e^(n+1) −1)=+∞ (diverges).](https://www.tinkutara.com/question/Q180705.png)
$$\int_{\mathrm{0}} ^{\infty} {e}^{\left[{x}\right]} {dx}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {e}^{{x}} {dx}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left({e}^{{k}+\mathrm{1}} −{e}^{{k}} \right) \\ $$$$=\left({e}−\mathrm{1}\right)+\left({e}^{\mathrm{2}} −{e}\right)+\centerdot\centerdot\centerdot+\left({e}^{{n}} −{e}^{{n}−\mathrm{1}} \right)+\left({e}^{{n}+\mathrm{1}} −{e}^{{n}} \right)+… \\ $$$$=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\left({e}^{{n}+\mathrm{1}} −\mathrm{1}\right)=+\infty\:\:\left(\mathrm{diverges}\right). \\ $$
Commented by SANOGO last updated on 16/Nov/22
$${thank}\:{you} \\ $$
