Question Number 47188 by 23kpratik last updated on 06/Nov/18
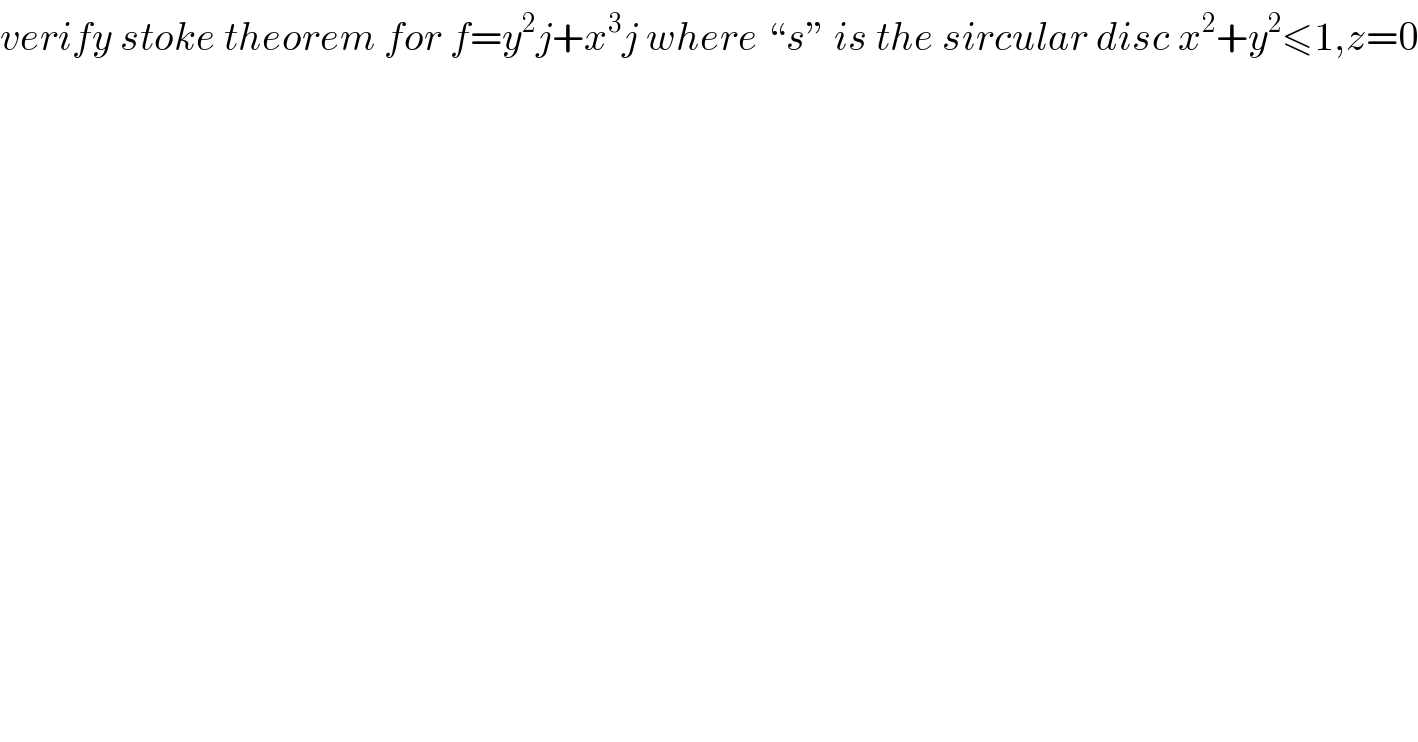
$${verify}\:{stoke}\:{theorem}\:{for}\:{f}={y}^{\mathrm{2}} {j}+{x}^{\mathrm{3}} {j}\:{where}\:“{s}''\:{is}\:{the}\:{sircular}\:{disc}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant\mathrm{1},{z}=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Nov/18
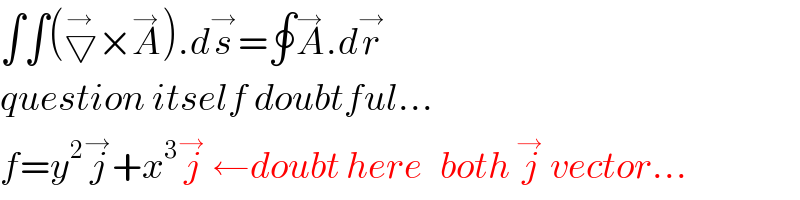
$$\int\int\left(\overset{\rightarrow} {\bigtriangledown}×\overset{\rightarrow} {{A}}\right).{d}\overset{\rightarrow} {{s}}=\oint\overset{\rightarrow} {{A}}.{d}\overset{\rightarrow} {{r}} \\ $$$${question}\:{itself}\:{doubtful}… \\ $$$${f}={y}^{\mathrm{2}} \overset{\rightarrow} {{j}}+{x}^{\mathrm{3}} \overset{\rightarrow} {{j}}\:\leftarrow{doubt}\:{here}\:\:\:{both}\:\overset{\rightarrow} {{j}}\:{vector}… \\ $$
