verify-the-formulae-n-1-na-1-p-pi-a-n-lim-z-1-a-1-p-1-cotan-piz-p-1-inthis-case-1-a-1-and-p-2-2-a-2-and-p-2-3-a-2-and-p-3-4-a-3-and-p-2-

Question Number 110954 by mathmax by abdo last updated on 01/Sep/20

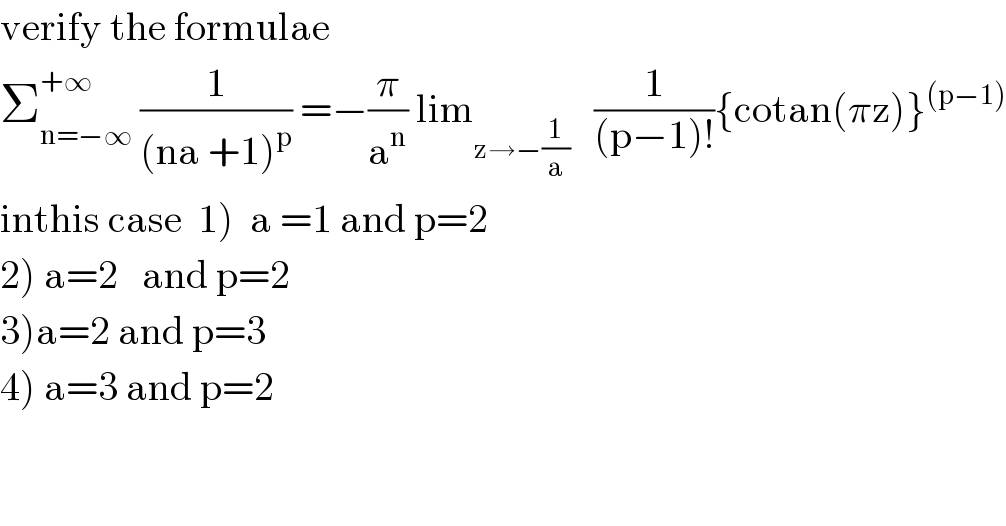
$$\mathrm{verify}\:\mathrm{the}\:\mathrm{formulae} \\ $$$$\sum_{\mathrm{n}=−\infty} ^{+\infty} \:\frac{\mathrm{1}}{\left(\mathrm{na}\:+\mathrm{1}\right)^{\mathrm{p}} }\:=−\frac{\pi}{\mathrm{a}^{\mathrm{n}} }\:\mathrm{lim}_{\mathrm{z}\rightarrow−\frac{\mathrm{1}}{\mathrm{a}}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{p}−\mathrm{1}\right)!}\left\{\mathrm{cotan}\left(\pi\mathrm{z}\right)\right\}^{\left(\mathrm{p}−\mathrm{1}\right)} \\ $$$$\left.\mathrm{inthis}\:\mathrm{case}\:\:\mathrm{1}\right)\:\:\mathrm{a}\:=\mathrm{1}\:\mathrm{and}\:\mathrm{p}=\mathrm{2} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{a}=\mathrm{2}\:\:\:\mathrm{and}\:\mathrm{p}=\mathrm{2} \\ $$$$\left.\mathrm{3}\right)\mathrm{a}=\mathrm{2}\:\mathrm{and}\:\mathrm{p}=\mathrm{3} \\ $$$$\left.\mathrm{4}\right)\:\mathrm{a}=\mathrm{3}\:\mathrm{and}\:\mathrm{p}=\mathrm{2} \\ $$

Answered by mathmax by abdo last updated on 01/Sep/20

$$\mathrm{sorry}\:−\frac{\pi}{\mathrm{a}^{\mathrm{p}} } \\ $$

Commented by khaki last updated on 01/Sep/20

please solve one quation evaluate the integral. ax+b/ax2+bx+c

Terms of Service
Privacy Policy
Contact: info@tinkutara.com