Question Number 102139 by mathocean1 last updated on 06/Jul/20
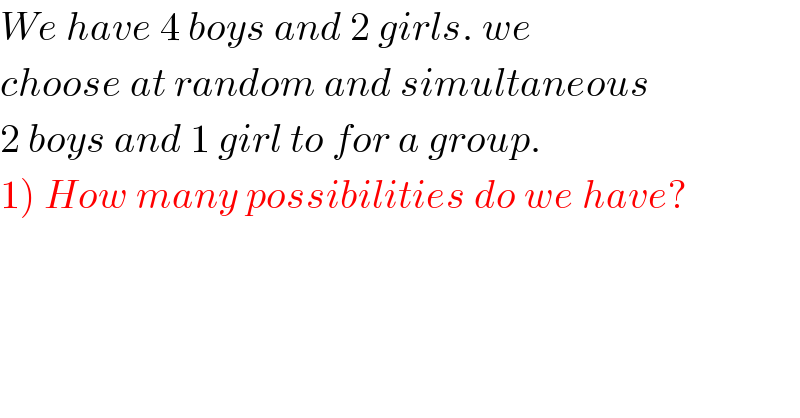
$${We}\:{have}\:\mathrm{4}\:{boys}\:{and}\:\mathrm{2}\:{girls}.\:{we} \\ $$$${choose}\:{at}\:{random}\:{and}\:{simultaneous} \\ $$$$\mathrm{2}\:{boys}\:{and}\:\mathrm{1}\:{girl}\:{to}\:{for}\:{a}\:{group}. \\ $$$$\left.\mathrm{1}\right)\:{How}\:{many}\:{possibilities}\:{do}\:{we}\:{have}? \\ $$
Commented by prakash jain last updated on 07/Jul/20

$$\:^{\mathrm{4}} {C}_{\mathrm{2}} ×^{\mathrm{2}} {C}_{\mathrm{1}} =\mathrm{24}. \\ $$
Answered by geoplitz last updated on 06/Jul/20
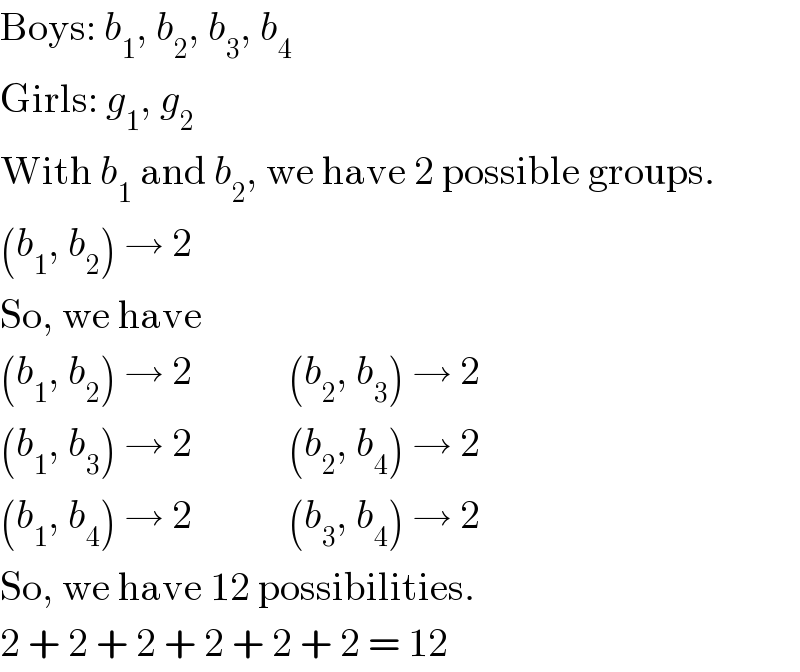
$$\mathrm{Boys}:\:{b}_{\mathrm{1}} ,\:{b}_{\mathrm{2}} ,\:{b}_{\mathrm{3}} ,\:{b}_{\mathrm{4}} \\ $$$$\mathrm{Girls}:\:{g}_{\mathrm{1}} ,\:{g}_{\mathrm{2}} \\ $$$$\mathrm{With}\:{b}_{\mathrm{1}} \:\mathrm{and}\:{b}_{\mathrm{2}} ,\:\mathrm{we}\:\mathrm{have}\:\mathrm{2}\:\mathrm{possible}\:\mathrm{groups}. \\ $$$$\left({b}_{\mathrm{1}} ,\:{b}_{\mathrm{2}} \right)\:\rightarrow\:\mathrm{2} \\ $$$$\mathrm{So},\:\mathrm{we}\:\mathrm{have} \\ $$$$\left({b}_{\mathrm{1}} ,\:{b}_{\mathrm{2}} \right)\:\rightarrow\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\left({b}_{\mathrm{2}} ,\:{b}_{\mathrm{3}} \right)\:\rightarrow\:\mathrm{2} \\ $$$$\left({b}_{\mathrm{1}} ,\:{b}_{\mathrm{3}} \right)\:\rightarrow\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\left({b}_{\mathrm{2}} ,\:{b}_{\mathrm{4}} \right)\:\rightarrow\:\mathrm{2} \\ $$$$\left({b}_{\mathrm{1}} ,\:{b}_{\mathrm{4}} \right)\:\rightarrow\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\left({b}_{\mathrm{3}} ,\:{b}_{\mathrm{4}} \right)\:\rightarrow\:\mathrm{2} \\ $$$$\mathrm{So},\:\mathrm{we}\:\mathrm{have}\:\mathrm{12}\:\mathrm{possibilities}. \\ $$$$\mathrm{2}\:+\:\mathrm{2}\:+\:\mathrm{2}\:+\:\mathrm{2}\:+\:\mathrm{2}\:+\:\mathrm{2}\:=\:\mathrm{12} \\ $$
