Question Number 93963 by M±th+et+s last updated on 16/May/20
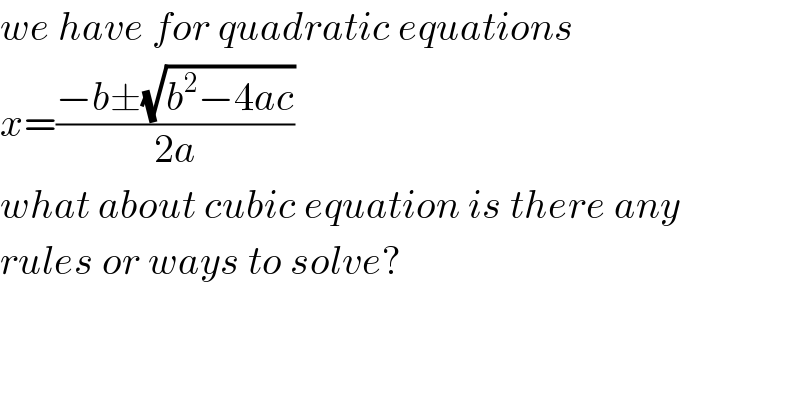
$${we}\:{have}\:{for}\:{quadratic}\:{equations} \\ $$$${x}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$${what}\:{about}\:{cubic}\:{equation}\:{is}\:{there}\:{any} \\ $$$${rules}\:{or}\:{ways}\:{to}\:{solve}? \\ $$
Commented by Kunal12588 last updated on 16/May/20
![for the roots I heard there is a formula for cubic too but it is too long to be remembered. same for biquadratic.[don′t know for higher] but there are methods to solve like cardano and trigonometric [I heard of Farrari too, I think it′s for biquadratic]](https://www.tinkutara.com/question/Q93965.png)
$${for}\:{the}\:{roots}\:{I}\:{heard}\:{there}\:{is}\:{a}\:{formula}\:{for} \\ $$$${cubic}\:{too}\:{but}\:{it}\:{is}\:{too}\:{long}\:{to}\:{be}\:{remembered}. \\ $$$${same}\:{for}\:{biquadratic}.\left[{don}'{t}\:{know}\:{for}\:{higher}\right] \\ $$$${but}\:{there}\:{are}\:{methods}\:{to}\:{solve}\:{like}\:{cardano}\:{and} \\ $$$${trigonometric}\:\left[{I}\:{heard}\:{of}\:{Farrari}\:{too},\:{I}\:{think}\right. \\ $$$$\left.{it}'{s}\:{for}\:{biquadratic}\right] \\ $$
Commented by mr W last updated on 16/May/20

$${see}\:{Q}\mathrm{89687} \\ $$
Commented by mr W last updated on 16/May/20
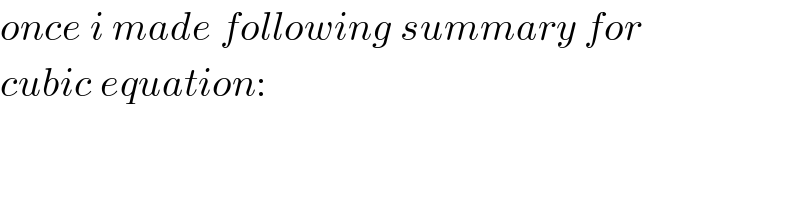
$${once}\:{i}\:{made}\:{following}\:{summary}\:{for} \\ $$$${cubic}\:{equation}: \\ $$
Commented by mr W last updated on 16/May/20
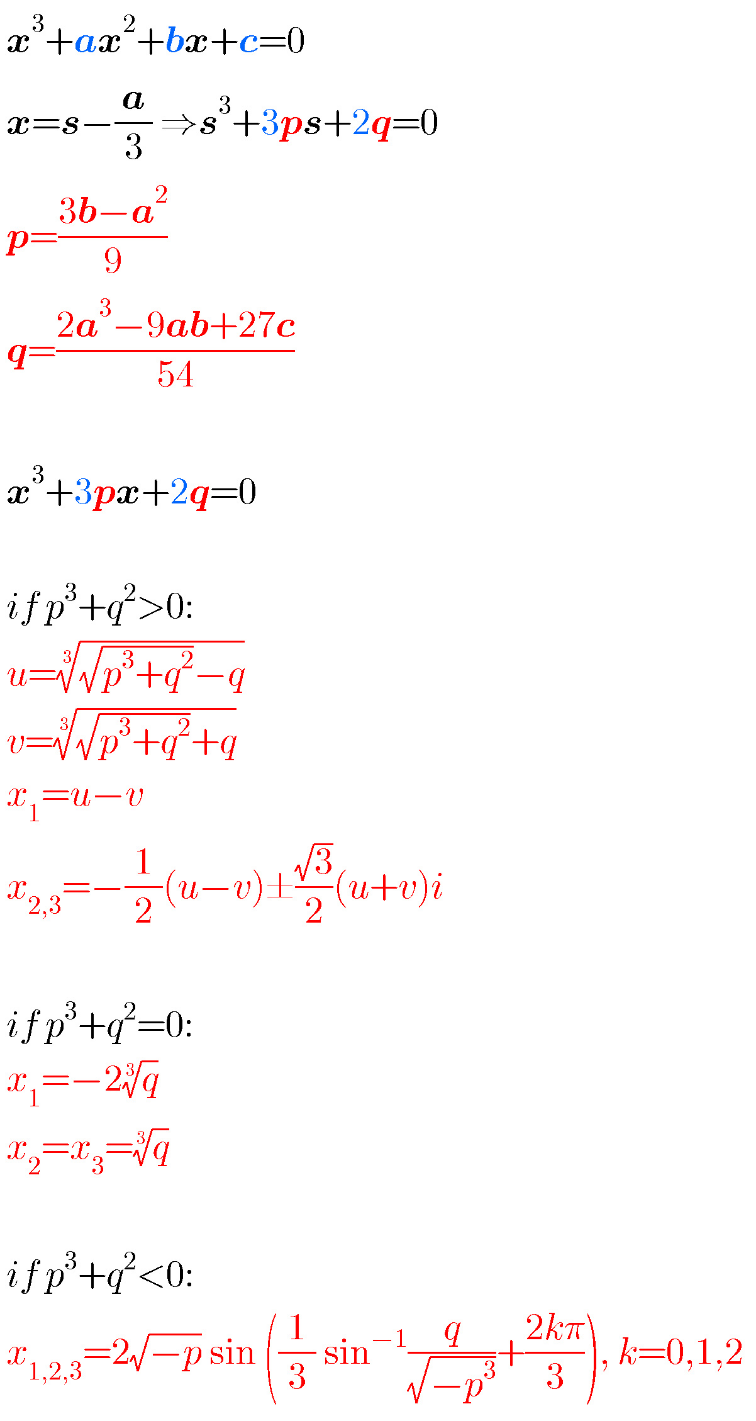
Commented by M±th+et+s last updated on 16/May/20

$${thank}\:{you}\:{sir} \\ $$
Commented by Tony Lin last updated on 16/May/20

Commented by Tony Lin last updated on 16/May/20

Commented by Tony Lin last updated on 16/May/20

Commented by Tony Lin last updated on 16/May/20

$${we}\:{still}\:{can}\:{get}\:{the}\:{formula}\:{of}\:{cubic} \\ $$$${and}\:{biquadratic}\:{in}\:{terms}\:{of}\:{a},{b},{c},{d},{e} \\ $$$${but}\:{they}\:{are}\:{too}\:{hard}\:{to}\:{remember}\:, \\ $$$${which}\:{is}\:{totally}\:{not}\:{useful} \\ $$
Commented by M±th+et+s last updated on 16/May/20

$${thank}\:{you}\:{sir}\: \\ $$
Commented by M±th+et+s last updated on 16/May/20
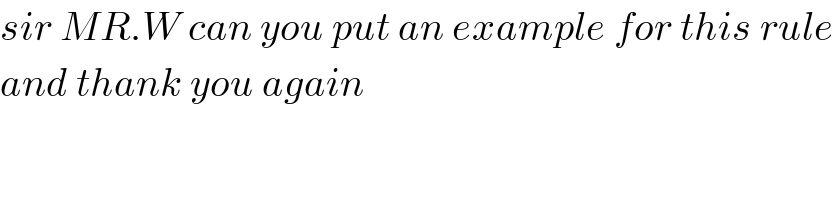
$${sir}\:{MR}.{W}\:{can}\:{you}\:{put}\:{an}\:{example}\:{for}\:{this}\:{rule} \\ $$$${and}\:{thank}\:{you}\:{again} \\ $$
Commented by mr W last updated on 16/May/20
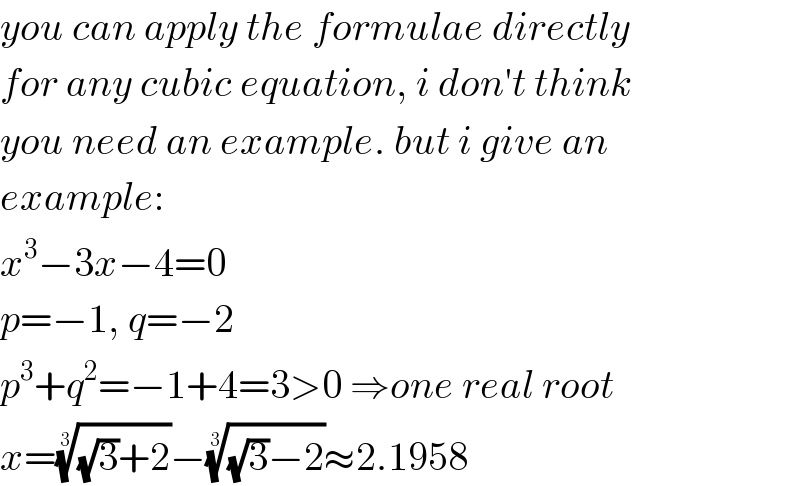
$${you}\:{can}\:{apply}\:{the}\:{formulae}\:{directly}\: \\ $$$${for}\:{any}\:{cubic}\:{equation},\:{i}\:{don}'{t}\:{think} \\ $$$${you}\:{need}\:{an}\:{example}.\:{but}\:{i}\:{give}\:{an} \\ $$$${example}: \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$${p}=−\mathrm{1},\:{q}=−\mathrm{2} \\ $$$${p}^{\mathrm{3}} +{q}^{\mathrm{2}} =−\mathrm{1}+\mathrm{4}=\mathrm{3}>\mathrm{0}\:\Rightarrow{one}\:{real}\:{root} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{3}}+\mathrm{2}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{3}}−\mathrm{2}}\approx\mathrm{2}.\mathrm{1958} \\ $$
