Question Number 114857 by Rio Michael last updated on 21/Sep/20

$$\mathrm{we}\:\mathrm{know}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:{e}^{\pi{i}} \:=\:−\mathrm{1}\: \\ $$$$\Rightarrow\:\mathrm{ln}\:\left({e}^{\pi{i}} \right)\:=\:\mathrm{ln}\left(−\mathrm{1}\right) \\ $$$$\:\:\pi{i}\:=\:\mathrm{ln}\:\left(−\mathrm{1}\right).\: \\ $$$$\mathrm{How}\:\mathrm{good}\:\mathrm{is}\:\mathrm{this}\:\mathrm{prove}? \\ $$
Commented by malwan last updated on 21/Sep/20
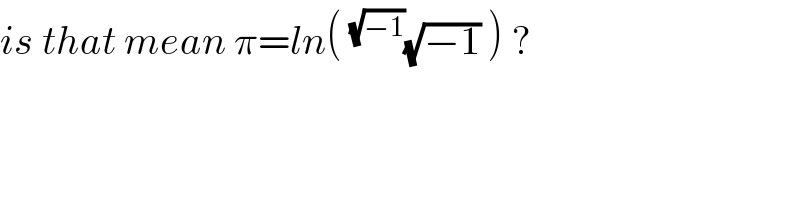
$${is}\:{that}\:{mean}\:\pi={ln}\left(\:^{\sqrt{−\mathrm{1}}} \sqrt{−\mathrm{1}}\:\right)\:? \\ $$
Commented by mr W last updated on 21/Sep/20

$${you}\:{can}\:{even}\:{say} \\ $$$$\pi=\mathrm{ln}\:\sqrt[{{i}}]{−\mathrm{1}} \\ $$
Commented by Rio Michael last updated on 21/Sep/20

$$\mathrm{really}\:\mathrm{sir}? \\ $$
Commented by MJS_new last updated on 21/Sep/20
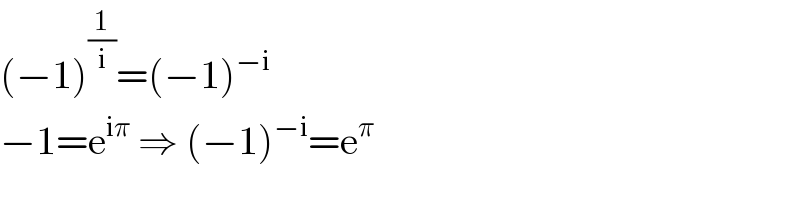
$$\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{i}}} =\left(−\mathrm{1}\right)^{−\mathrm{i}} \\ $$$$−\mathrm{1}=\mathrm{e}^{\mathrm{i}\pi} \:\Rightarrow\:\left(−\mathrm{1}\right)^{−\mathrm{i}} =\mathrm{e}^{\pi} \\ $$
Commented by Rio Michael last updated on 21/Sep/20

$$\mathrm{thanks}\:\mathrm{prof} \\ $$
Commented by Dwaipayan Shikari last updated on 21/Sep/20
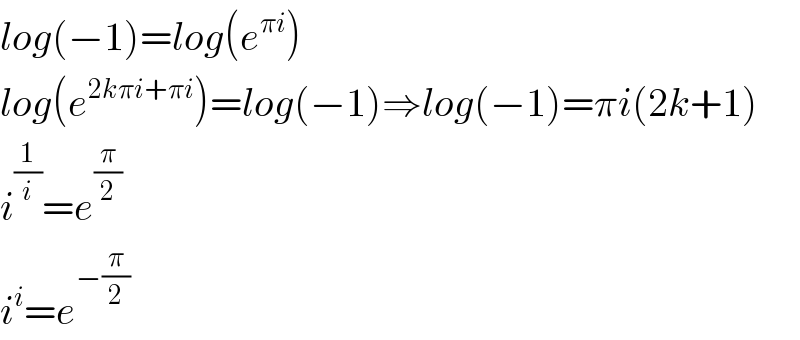
$${log}\left(−\mathrm{1}\right)={log}\left({e}^{\pi{i}} \right) \\ $$$${log}\left({e}^{\mathrm{2}{k}\pi{i}+\pi{i}} \right)={log}\left(−\mathrm{1}\right)\Rightarrow{log}\left(−\mathrm{1}\right)=\pi{i}\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$${i}^{\frac{\mathrm{1}}{{i}}} ={e}^{\frac{\pi}{\mathrm{2}}} \\ $$$${i}^{{i}} ={e}^{−\frac{\pi}{\mathrm{2}}} \\ $$
Commented by MJS_new last updated on 21/Sep/20

$$\mathrm{yes} \\ $$
