Menu Close

what-is-coefficient-of-x-2-in-1-x-1-2x-1-3x-1-4x-1-5x-1-14x-1-15x-

Tinku Tara 0 Comments
Pin




Question Number 177822 by cortano1 last updated on 09/Oct/22
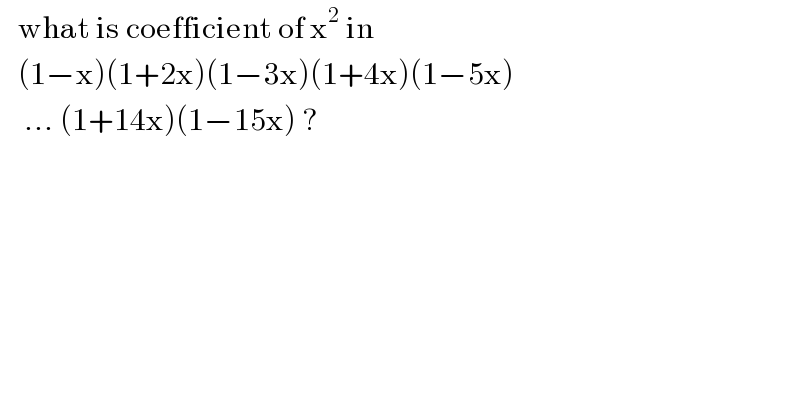
what is coefficient of x^2 in (1−x)(1+2x)(1−3x)(1+4x)(1−5x) ... (1+14x)(1−15x) ?
$$\:\:\:\mathrm{what}\:\mathrm{is}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{in}\: \\ $$$$\:\:\:\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{2x}\right)\left(\mathrm{1}−\mathrm{3x}\right)\left(\mathrm{1}+\mathrm{4x}\right)\left(\mathrm{1}−\mathrm{5x}\right) \\ $$$$\:\:\:\:…\:\left(\mathrm{1}+\mathrm{14x}\right)\left(\mathrm{1}−\mathrm{15x}\right)\:? \\ $$
Commented by mr W last updated on 10/Oct/22
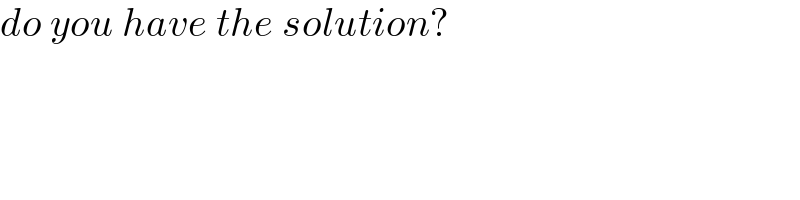
do you have the solution?
$${do}\:{you}\:{have}\:{the}\:{solution}? \\ $$
Commented by cortano1 last updated on 11/Oct/22
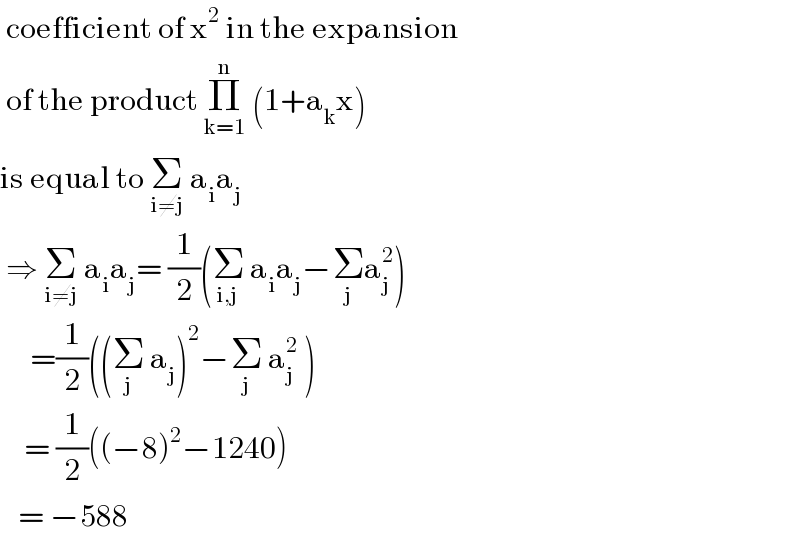
coefficient of x^2 in the expansion of the product Π_(k=1) ^n (1+a_k x) is equal to Σ_(i≠j) a_i a_j ⇒ Σ_(i≠j) a_i a_j = (1/2)(Σ_(i,j) a_i a_j −Σ_j a_j ^2 ) =(1/2)((Σ_j a_j )^2 −Σ_j a_j ^2 ) = (1/2)((−8)^2 −1240) = −588
$$\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion} \\ $$$$\:\mathrm{of}\:\mathrm{the}\:\mathrm{product}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\:\left(\mathrm{1}+\mathrm{a}_{\mathrm{k}} \mathrm{x}\right) \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\underset{\mathrm{i}\neq\mathrm{j}} {\sum}\:\mathrm{a}_{\mathrm{i}} \mathrm{a}_{\mathrm{j}} \: \\ $$$$\:\Rightarrow\:\underset{\mathrm{i}\neq\mathrm{j}} {\sum}\:\mathrm{a}_{\mathrm{i}} \mathrm{a}_{\mathrm{j}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{\mathrm{i},\mathrm{j}} {\sum}\:\mathrm{a}_{\mathrm{i}} \mathrm{a}_{\mathrm{j}} −\underset{\mathrm{j}} {\sum}\mathrm{a}_{\mathrm{j}} ^{\mathrm{2}} \right)\: \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\left(\underset{\mathrm{j}} {\sum}\:\mathrm{a}_{\mathrm{j}} \right)^{\mathrm{2}} −\underset{\mathrm{j}} {\sum}\:\mathrm{a}_{\mathrm{j}} ^{\mathrm{2}} \:\right) \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\left(−\mathrm{8}\right)^{\mathrm{2}} −\mathrm{1240}\right) \\ $$$$\:\:\:=\:−\mathrm{588} \\ $$
Answered by mr W last updated on 09/Oct/22
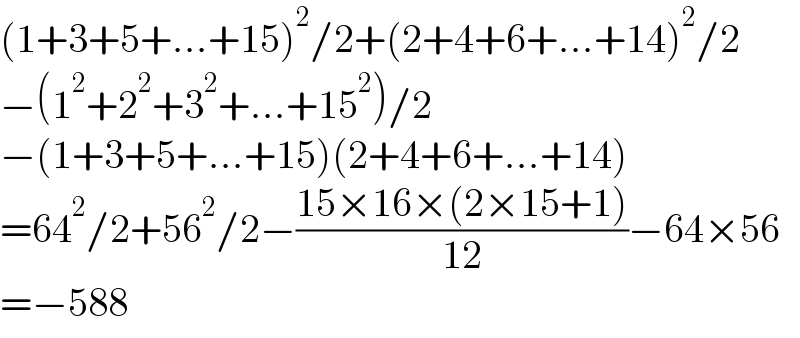
(1+3+5+...+15)^2 /2+(2+4+6+...+14)^2 /2 −(1^2 +2^2 +3^2 +...+15^2 )/2 −(1+3+5+...+15)(2+4+6+...+14) =64^2 /2+56^2 /2−((15×16×(2×15+1))/(12))−64×56 =−588
$$\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\mathrm{15}\right)^{\mathrm{2}} /\mathrm{2}+\left(\mathrm{2}+\mathrm{4}+\mathrm{6}+…+\mathrm{14}\right)^{\mathrm{2}} /\mathrm{2} \\ $$$$−\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +…+\mathrm{15}^{\mathrm{2}} \right)/\mathrm{2} \\ $$$$−\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\mathrm{15}\right)\left(\mathrm{2}+\mathrm{4}+\mathrm{6}+…+\mathrm{14}\right) \\ $$$$=\mathrm{64}^{\mathrm{2}} /\mathrm{2}+\mathrm{56}^{\mathrm{2}} /\mathrm{2}−\frac{\mathrm{15}×\mathrm{16}×\left(\mathrm{2}×\mathrm{15}+\mathrm{1}\right)}{\mathrm{12}}−\mathrm{64}×\mathrm{56} \\ $$$$=−\mathrm{588} \\ $$
Commented by Tawa11 last updated on 10/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by cortano1 last updated on 11/Oct/22
yes −588
$$\mathrm{yes}\:−\mathrm{588} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *