Question Number 181841 by mr W last updated on 01/Dec/22
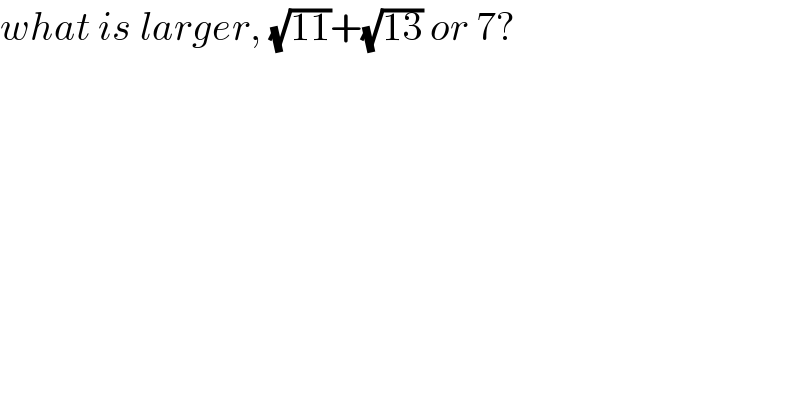
$${what}\:{is}\:{larger},\:\sqrt{\mathrm{11}}+\sqrt{\mathrm{13}}\:{or}\:\mathrm{7}? \\ $$
Answered by hmr last updated on 01/Dec/22

$$ \\ $$$${assume}\:{that}:\: \\ $$$$\sqrt{\mathrm{11}}\:+\:\sqrt{\mathrm{13}\:}\:<\:\mathrm{7} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{11}\:+\:\mathrm{2}\sqrt{\mathrm{143}}\:+\:\mathrm{13}\:<\:\mathrm{49} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{24}\:+\:\mathrm{2}\sqrt{\mathrm{143}}\:<\:\mathrm{49} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{2}\sqrt{\mathrm{143}}\:<\:\mathrm{25} \\ $$$$\Leftrightarrow \\ $$$$\sqrt{\mathrm{143}}\:<\:\mathrm{12}.\mathrm{5} \\ $$$${and}\:{this}\:{is}\:{always}\:{true} \\ $$$${because}\:\sqrt{\mathrm{143}}\:<\:\sqrt{\mathrm{144}}\:=\:\mathrm{12} \\ $$$${and}\:\mathrm{12}\:<\:\mathrm{12}.\mathrm{5} \\ $$$${so}\:\sqrt{\mathrm{143}}\:<\:\mathrm{12}.\mathrm{5} \\ $$$${and}\:{it}\:{is}\:{equal}\:{to}\:\sqrt{\mathrm{11}\:}+\:\sqrt{\mathrm{13}}\:<\:\mathrm{7} \\ $$
Commented by mr W last updated on 01/Dec/22

$${thanks}! \\ $$
Commented by hmr last updated on 01/Dec/22

$${you}'{re}\:{welcome}\: \\ $$
Answered by BaliramKumar last updated on 01/Dec/22
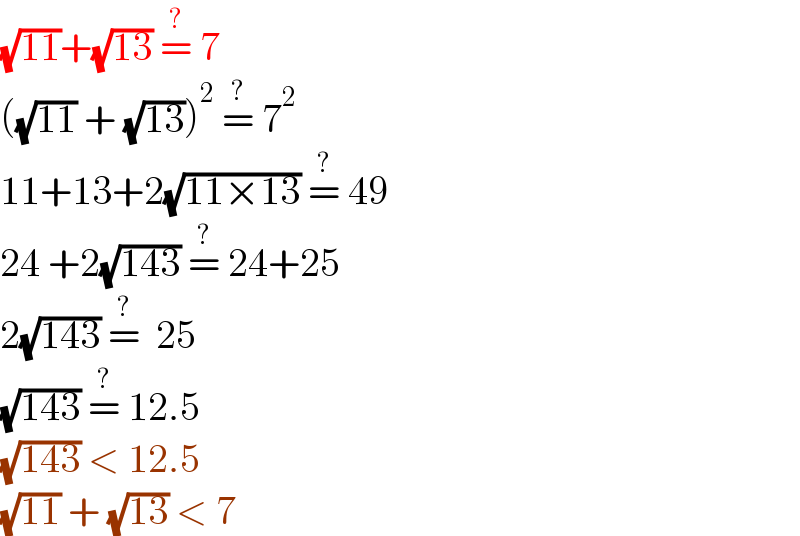
$$\sqrt{\mathrm{11}}+\sqrt{\mathrm{13}}\:\overset{?} {=}\:\mathrm{7} \\ $$$$\left(\sqrt{\mathrm{11}}\:+\:\sqrt{\mathrm{13}}\right)^{\mathrm{2}} \:\overset{?} {=}\:\mathrm{7}^{\mathrm{2}} \\ $$$$\mathrm{11}+\mathrm{13}+\mathrm{2}\sqrt{\mathrm{11}×\mathrm{13}}\:\overset{?} {=}\:\mathrm{49} \\ $$$$\mathrm{24}\:+\mathrm{2}\sqrt{\mathrm{143}}\:\overset{?} {=}\:\mathrm{24}+\mathrm{25} \\ $$$$\mathrm{2}\sqrt{\mathrm{143}}\:\overset{?} {=}\:\:\mathrm{25} \\ $$$$\sqrt{\mathrm{143}}\:\overset{?} {=}\:\mathrm{12}.\mathrm{5} \\ $$$$\sqrt{\mathrm{143}}\:<\:\mathrm{12}.\mathrm{5} \\ $$$$\sqrt{\mathrm{11}}\:+\:\sqrt{\mathrm{13}}\:<\:\mathrm{7} \\ $$
Commented by mr W last updated on 01/Dec/22

$${thanks}! \\ $$
Answered by mr W last updated on 01/Dec/22
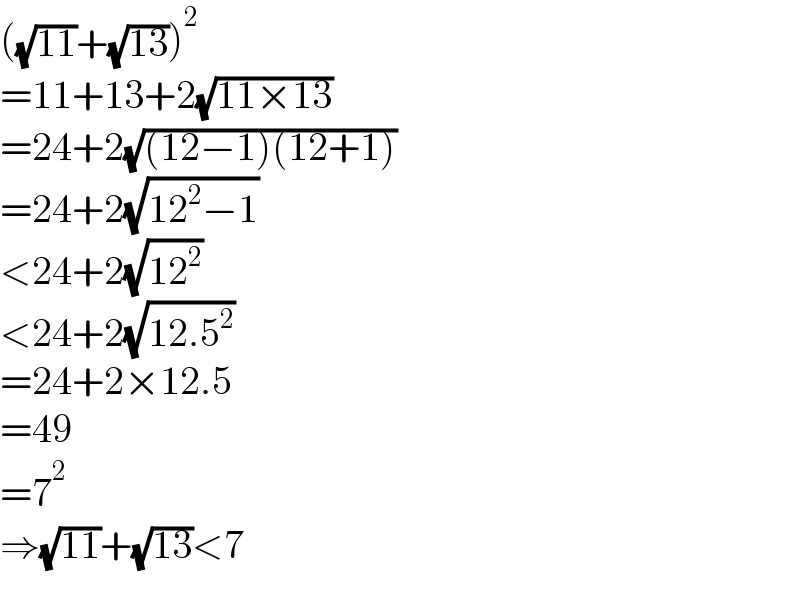
$$\left(\sqrt{\mathrm{11}}+\sqrt{\mathrm{13}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{11}+\mathrm{13}+\mathrm{2}\sqrt{\mathrm{11}×\mathrm{13}} \\ $$$$=\mathrm{24}+\mathrm{2}\sqrt{\left(\mathrm{12}−\mathrm{1}\right)\left(\mathrm{12}+\mathrm{1}\right)} \\ $$$$=\mathrm{24}+\mathrm{2}\sqrt{\mathrm{12}^{\mathrm{2}} −\mathrm{1}} \\ $$$$<\mathrm{24}+\mathrm{2}\sqrt{\mathrm{12}^{\mathrm{2}} } \\ $$$$<\mathrm{24}+\mathrm{2}\sqrt{\mathrm{12}.\mathrm{5}^{\mathrm{2}} } \\ $$$$=\mathrm{24}+\mathrm{2}×\mathrm{12}.\mathrm{5} \\ $$$$=\mathrm{49} \\ $$$$=\mathrm{7}^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{11}}+\sqrt{\mathrm{13}}<\mathrm{7} \\ $$
