Question Number 183660 by mr W last updated on 28/Dec/22
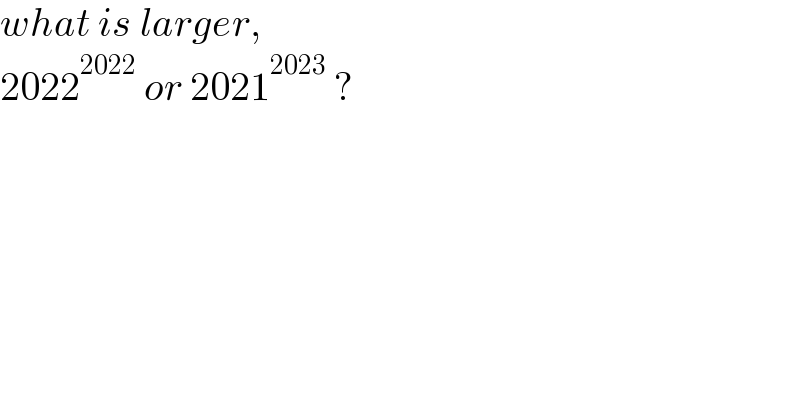
$${what}\:{is}\:{larger}, \\ $$$$\mathrm{2022}^{\mathrm{2022}} \:{or}\:\mathrm{2021}^{\mathrm{2023}} \:? \\ $$
Answered by Ar Brandon last updated on 28/Dec/22
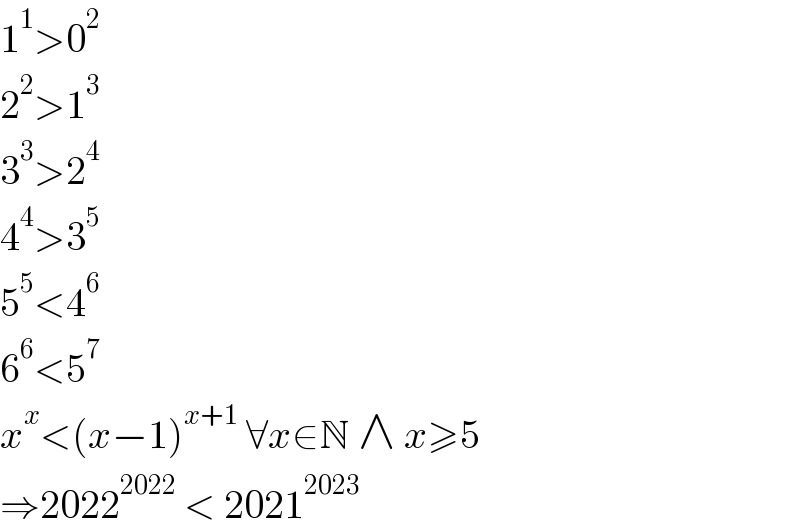
$$\mathrm{1}^{\mathrm{1}} >\mathrm{0}^{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{2}} >\mathrm{1}^{\mathrm{3}} \\ $$$$\mathrm{3}^{\mathrm{3}} >\mathrm{2}^{\mathrm{4}} \\ $$$$\mathrm{4}^{\mathrm{4}} >\mathrm{3}^{\mathrm{5}} \\ $$$$\mathrm{5}^{\mathrm{5}} <\mathrm{4}^{\mathrm{6}} \\ $$$$\mathrm{6}^{\mathrm{6}} <\mathrm{5}^{\mathrm{7}} \\ $$$${x}^{{x}} <\left({x}−\mathrm{1}\right)^{{x}+\mathrm{1}} \:\forall{x}\in\mathbb{N}\:\wedge\:{x}\geqslant\mathrm{5} \\ $$$$\Rightarrow\mathrm{2022}^{\mathrm{2022}} \:<\:\mathrm{2021}^{\mathrm{2023}} \\ $$
Answered by manxsol last updated on 29/Dec/22

$$\mathrm{2022}^{\mathrm{2022}} {and}\:\mathrm{2021}×\mathrm{2021}^{\mathrm{2022}} \\ $$$$\frac{\mathrm{2022}^{\mathrm{2022}} }{\mathrm{2021}^{\mathrm{2022}} }\:\:{and}\:\mathrm{2021} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2021}}\right)^{\mathrm{2022}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2021}}\right)^{\mathrm{2021}} ×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2021}}\right) \\ $$$$={e}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2021}}\right)={e}+\frac{{e}}{\mathrm{2021}} \\ $$$${e}+\frac{{e}}{\mathrm{2021}}\:<\mathrm{2021} \\ $$$$\mathrm{2022}^{\mathrm{2022}} \:\langle\:\:\mathrm{2021}^{\mathrm{2023}} \\ $$$${theory} \\ $$$${li}\underset{{x}\rightarrow\infty} {{m}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} ={e}=\mathrm{2}.\mathrm{71}… \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 28/Dec/22
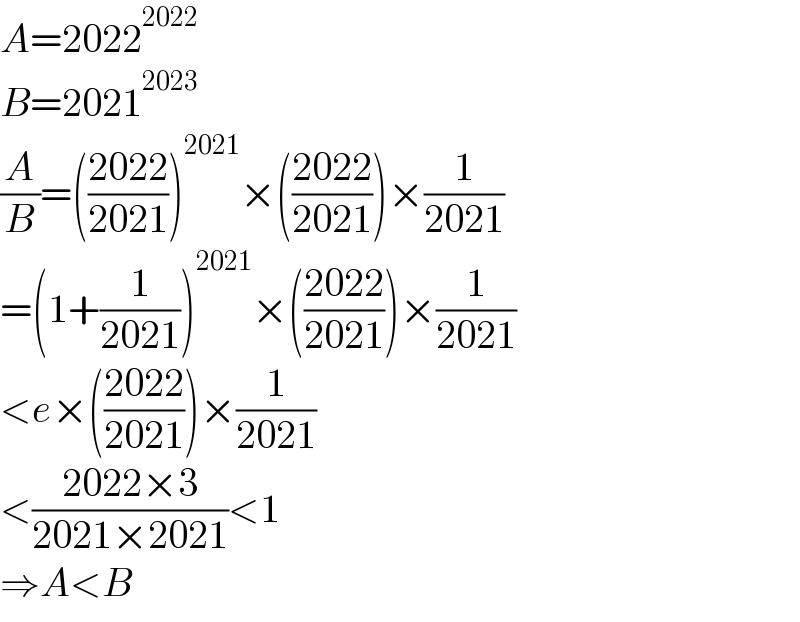
$${A}=\mathrm{2022}^{\mathrm{2022}} \\ $$$${B}=\mathrm{2021}^{\mathrm{2023}} \\ $$$$\frac{{A}}{{B}}=\left(\frac{\mathrm{2022}}{\mathrm{2021}}\right)^{\mathrm{2021}} ×\left(\frac{\mathrm{2022}}{\mathrm{2021}}\right)×\frac{\mathrm{1}}{\mathrm{2021}} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2021}}\right)^{\mathrm{2021}} ×\left(\frac{\mathrm{2022}}{\mathrm{2021}}\right)×\frac{\mathrm{1}}{\mathrm{2021}} \\ $$$$<{e}×\left(\frac{\mathrm{2022}}{\mathrm{2021}}\right)×\frac{\mathrm{1}}{\mathrm{2021}} \\ $$$$<\frac{\mathrm{2022}×\mathrm{3}}{\mathrm{2021}×\mathrm{2021}}<\mathrm{1} \\ $$$$\Rightarrow{A}<{B} \\ $$
