Question Number 104659 by bobhans last updated on 23/Jul/20
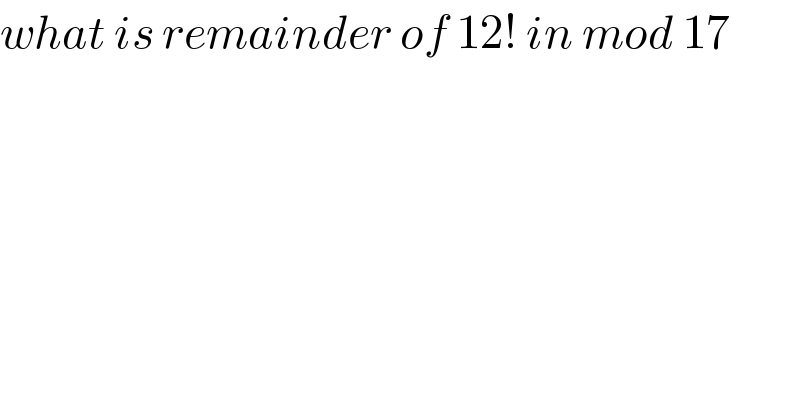
$${what}\:{is}\:{remainder}\:{of}\:\mathrm{12}!\:{in}\:{mod}\:\mathrm{17} \\ $$
Answered by bramlex last updated on 23/Jul/20

$${we}\:{can}\:{use}\:{Wilson}'{s}\:{theorem} \\ $$$${by}\:{which}\:\mathrm{16}!\:\equiv\:−\mathrm{1}\:\left({mod}\:\mathrm{17}\right) \\ $$$${Now}\:{use}\:{that}\: \\ $$$$\mathrm{16}!\:=\:\mathrm{16}.\mathrm{15}.\mathrm{14}.\mathrm{13}.\mathrm{12}! \\ $$$$\mathrm{16}!\:\equiv\:\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)\left(−\mathrm{4}\right).\mathrm{12}! \\ $$$$\left({mod}\:\mathrm{17}\:\right)\equiv\:\mathrm{12}!.\mathrm{7}\:\:\left({mod}\:\mathrm{17}\right) \\ $$$${because}\:\mathrm{7}.\mathrm{5}\:\equiv\:\mathrm{1}\:\left({mod}\:\mathrm{17}\right)\: \\ $$$${we}\:{get}\:\mathrm{12}!\:\equiv\:−\mathrm{5}\:\equiv\:\mathrm{12}\:\left({mod}\:\mathrm{17}\right) \\ $$$$ \\ $$
