Question Number 81286 by jagoll last updated on 11/Feb/20
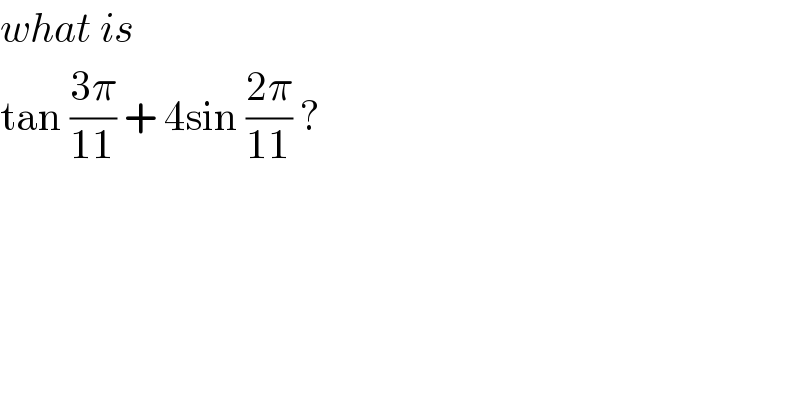
$${what}\:{is}\: \\ $$$$\mathrm{tan}\:\frac{\mathrm{3}\pi}{\mathrm{11}}\:+\:\mathrm{4sin}\:\frac{\mathrm{2}\pi}{\mathrm{11}}\:? \\ $$
Answered by MJS last updated on 11/Feb/20

$$\mathrm{a}\:\mathrm{strange}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this} \\ $$$$\mathrm{sin}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{i}\alpha} −\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2i}};\:\mathrm{cos}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{i}\alpha} +\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}\pi}{\mathrm{11}}} ={u}^{\frac{\mathrm{3}}{\mathrm{2}}} \wedge\mathrm{e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{11}}} ={u} \\ $$$$\frac{\frac{{u}^{\frac{\mathrm{3}}{\mathrm{2}}} −{u}^{−\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{2i}}}{\frac{{u}^{\frac{\mathrm{3}}{\mathrm{2}}} +{u}^{−\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{2}}}+\mathrm{4}\frac{{u}−{u}^{−\mathrm{1}} }{\mathrm{2i}}={t}>\mathrm{0} \\ $$$$−\mathrm{i}\frac{\mathrm{2}{u}^{\mathrm{5}} +{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{3}} +\mathrm{2}{u}^{\mathrm{2}} −{u}−\mathrm{2}}{{u}^{\mathrm{4}} +{u}}={t} \\ $$$$\mathrm{squaring}\:\mathrm{this}\:\Rightarrow \\ $$$$−\frac{\left({u}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{u}^{\mathrm{4}} +\mathrm{3}{u}^{\mathrm{3}} +{u}^{\mathrm{2}} +\mathrm{3}{u}+\mathrm{2}\right)^{\mathrm{2}} }{{u}^{\mathrm{2}} \left({u}+\mathrm{1}\right)^{\mathrm{2}} \left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)^{\mathrm{2}} }={t}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{u}^{\mathrm{10}} +\mathrm{4}{u}^{\mathrm{9}} +\left({t}^{\mathrm{2}} −\mathrm{7}\right){u}^{\mathrm{8}} +\mathrm{4}{u}^{\mathrm{7}} +\mathrm{4}{u}^{\mathrm{6}} +\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{9}\right){u}^{\mathrm{5}} +\mathrm{4}{u}^{\mathrm{4}} +\mathrm{4}{u}^{\mathrm{3}} +\left({t}^{\mathrm{2}} −\mathrm{7}\right){u}^{\mathrm{2}} +\mathrm{4}{u}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{if}\:{t}^{\mathrm{2}} −\mathrm{7}=\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{9}\right)=\mathrm{4}\:\mathrm{this}\:\mathrm{would}\:\mathrm{be}\:\mathrm{nice} \\ $$$$\Rightarrow\:{t}=\pm\sqrt{\mathrm{11}}\:\mathrm{but}\:\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:{t}>\mathrm{0}\:\Rightarrow\:{t}=\sqrt{\mathrm{11}} \\ $$$$\Rightarrow \\ $$$${u}^{\mathrm{10}} +{u}^{\mathrm{9}} +{u}^{\mathrm{8}} +{u}^{\mathrm{7}} +{u}^{\mathrm{6}} +{u}^{\mathrm{5}} +{u}^{\mathrm{4}} +{u}^{\mathrm{3}} +{u}^{\mathrm{2}} +{u}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{multiplicate}\:\mathrm{with}\:\left({u}−\mathrm{1}\right) \\ $$$$\Rightarrow \\ $$$${u}^{\mathrm{11}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\:{u}=\mathrm{1}\:\vee\:{u}=\mathrm{e}^{\mathrm{i}\frac{{n}\pi}{\mathrm{11}}} \:\mathrm{with}\:{n}\in\mathbb{N}\wedge\mathrm{1}\leqslant{n}\leqslant\mathrm{10} \\ $$$$\mathrm{but}\:{u}=\mathrm{e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{11}}} \:\mathrm{which}\:\mathrm{indeed}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{and} \\ $$$${u}^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}\pi}{\mathrm{11}}} \:\mathrm{which}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\Rightarrow \\ $$$${t}=\sqrt{\mathrm{11}} \\ $$
Commented by jagoll last updated on 11/Feb/20
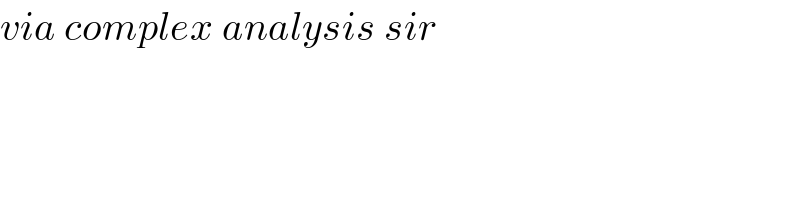
$${via}\:{complex}\:{analysis}\:{sir} \\ $$
