Menu Close

what-is-the-centre-of-the-circle-with-radius-4-2-that-can-be-inscribed-in-the-parabola-y-x-2-16x-128-

Tinku Tara 0 Comments
Pin




Question Number 117739 by bemath last updated on 13/Oct/20
what is the centre of the circle with radius 4(√2) that can be inscribed in the parabola y=x^2 −16x+128?
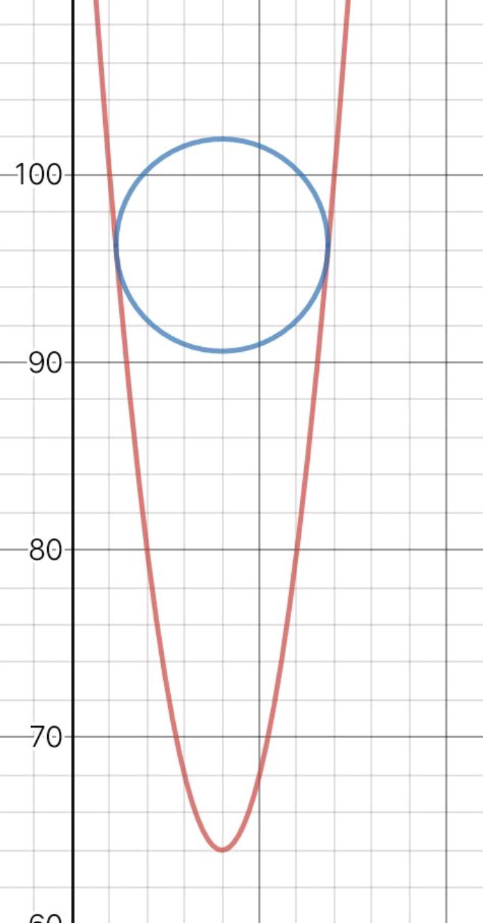
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$$\mathrm{with}\:\mathrm{radius}\:\mathrm{4}\sqrt{\mathrm{2}}\:\mathrm{that}\:\mathrm{can}\:\mathrm{be}\: \\ $$$$\mathrm{inscribed}\:\mathrm{in}\:\mathrm{the}\:\mathrm{parabola}\: \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{2}} −\mathrm{16x}+\mathrm{128}? \\ $$
Answered by bobhans last updated on 13/Oct/20
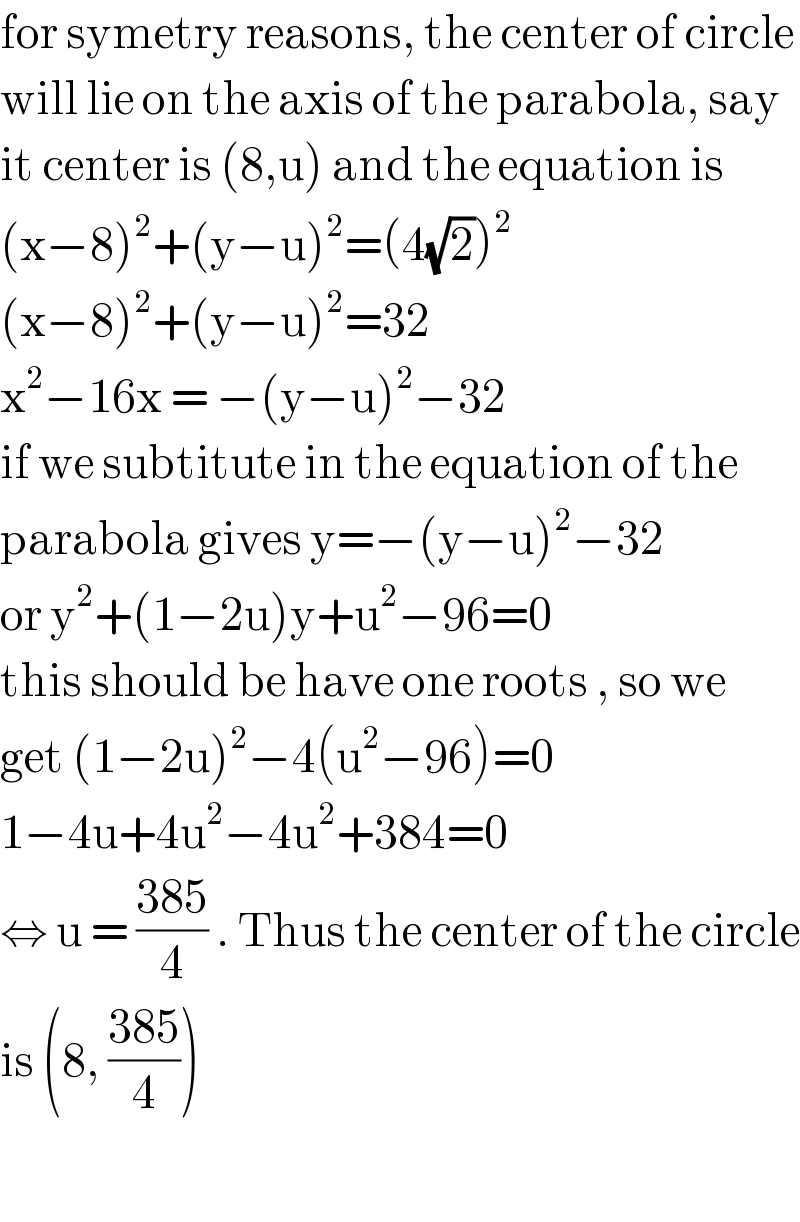
for symetry reasons, the center of circle will lie on the axis of the parabola, say it center is (8,u) and the equation is (x−8)^2 +(y−u)^2 =(4(√2))^2 (x−8)^2 +(y−u)^2 =32 x^2 −16x = −(y−u)^2 −32 if we subtitute in the equation of the parabola gives y=−(y−u)^2 −32 or y^2 +(1−2u)y+u^2 −96=0 this should be have one roots , so we get (1−2u)^2 −4(u^2 −96)=0 1−4u+4u^2 −4u^2 +384=0 ⇔ u = ((385)/4) . Thus the center of the circle is (8, ((385)/4))
$$\mathrm{for}\:\mathrm{symetry}\:\mathrm{reasons},\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{circle} \\ $$$$\mathrm{will}\:\mathrm{lie}\:\mathrm{on}\:\mathrm{the}\:\mathrm{axis}\:\mathrm{of}\:\mathrm{the}\:\mathrm{parabola},\:\mathrm{say} \\ $$$$\mathrm{it}\:\mathrm{center}\:\mathrm{is}\:\left(\mathrm{8},\mathrm{u}\right)\:\mathrm{and}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{is} \\ $$$$\left(\mathrm{x}−\mathrm{8}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{u}\right)^{\mathrm{2}} =\left(\mathrm{4}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{x}−\mathrm{8}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{u}\right)^{\mathrm{2}} =\mathrm{32} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{16x}\:=\:−\left(\mathrm{y}−\mathrm{u}\right)^{\mathrm{2}} −\mathrm{32} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{subtitute}\:\mathrm{in}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{parabola}\:\mathrm{gives}\:\mathrm{y}=−\left(\mathrm{y}−\mathrm{u}\right)^{\mathrm{2}} −\mathrm{32} \\ $$$$\mathrm{or}\:\mathrm{y}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{2u}\right)\mathrm{y}+\mathrm{u}^{\mathrm{2}} −\mathrm{96}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:\mathrm{have}\:\mathrm{one}\:\mathrm{roots}\:,\:\mathrm{so}\:\mathrm{we}\: \\ $$$$\mathrm{get}\:\left(\mathrm{1}−\mathrm{2u}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{96}\right)=\mathrm{0} \\ $$$$\mathrm{1}−\mathrm{4u}+\mathrm{4u}^{\mathrm{2}} −\mathrm{4u}^{\mathrm{2}} +\mathrm{384}=\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{u}\:=\:\frac{\mathrm{385}}{\mathrm{4}}\:.\:\mathrm{Thus}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$$\mathrm{is}\:\left(\mathrm{8},\:\frac{\mathrm{385}}{\mathrm{4}}\right) \\ $$$$ \\ $$
Commented by bemath last updated on 13/Oct/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *