Question Number 163576 by cortano1 last updated on 08/Jan/22
$$\:\:{What}\:{is}\:{the}\:{coefficient}\:{of}\:{x}^{\mathrm{2020}} \\ $$$$\:{in}\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{\mathrm{2020}} \right)^{\mathrm{2021}} \\ $$
Answered by bobhans last updated on 08/Jan/22
$$\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} +…+\mathrm{x}^{\mathrm{2020}} \right)^{\mathrm{2021}} \\ $$$$\:\:\mathrm{f}\left(\mathrm{x}\right)=\:\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)^{\mathrm{2021}} =\:\underset{\mathrm{m}=\mathrm{0}} {\overset{\mathrm{2021}} {\sum}}\:\begin{pmatrix}{\mathrm{2021}+\mathrm{m}−\mathrm{1}}\\{\:\:\:\:\:\:\:\:\:\:\:\mathrm{m}}\end{pmatrix}\:\mathrm{x}^{\mathrm{k}} \\ $$$$\:\mathrm{take}\:\mathrm{k}=\mathrm{2020}\:\Rightarrow\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2020}} =\:\begin{pmatrix}{\mathrm{4040}}\\{\mathrm{2020}}\end{pmatrix} \\ $$
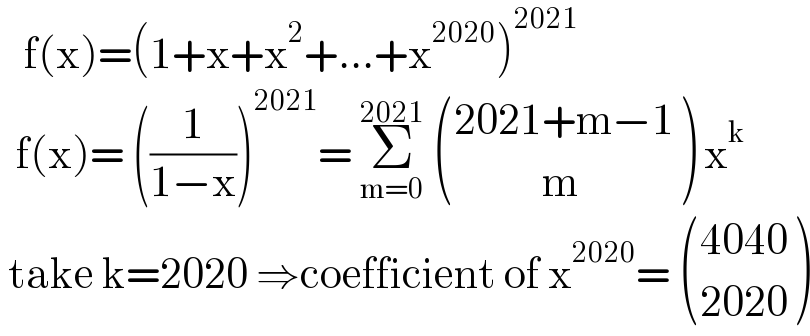
Answered by mr W last updated on 08/Jan/22
$${since}\:{you}\:{ask}\:{for}\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{2020}} , \\ $$$${you}\:{can}\:{add}\:{x}^{\mathrm{2021}} ,\:{x}^{\mathrm{2022}} ,\:…,\:\infty\:{into}\:{the} \\ $$$${expression}.\:{that}\:{wont}\:{change}\:{the} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{2020}} . \\ $$$${that}\:{means}\:{coef}.\:{of}\:{x}^{\mathrm{2020}} \:{in} \\ $$$$\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{\mathrm{2020}} \right)^{\mathrm{2021}} \:{is}\:{the} \\ $$$${same}\:{as}\:{coef}.\:{of}\:{x}^{\mathrm{2020}} \:{in} \\ $$$$\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{\mathrm{2020}} +{x}^{\mathrm{2021}} +…\right)^{\mathrm{2021}} .\: \\ $$$$ \\ $$$$\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{\mathrm{2020}} +{x}^{\mathrm{2021}} +…\right)^{\mathrm{2021}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)^{\mathrm{2021}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2020}} ^{{k}+\mathrm{2020}} {x}^{{k}} \\ $$$${the}\:{coef}.\:{of}\:{x}^{\mathrm{2020}} \:{is}\:{then} \\ $$$${C}_{\mathrm{2020}} ^{\mathrm{2020}+\mathrm{2020}} ={C}_{\mathrm{2020}} ^{\mathrm{4040}} \\ $$
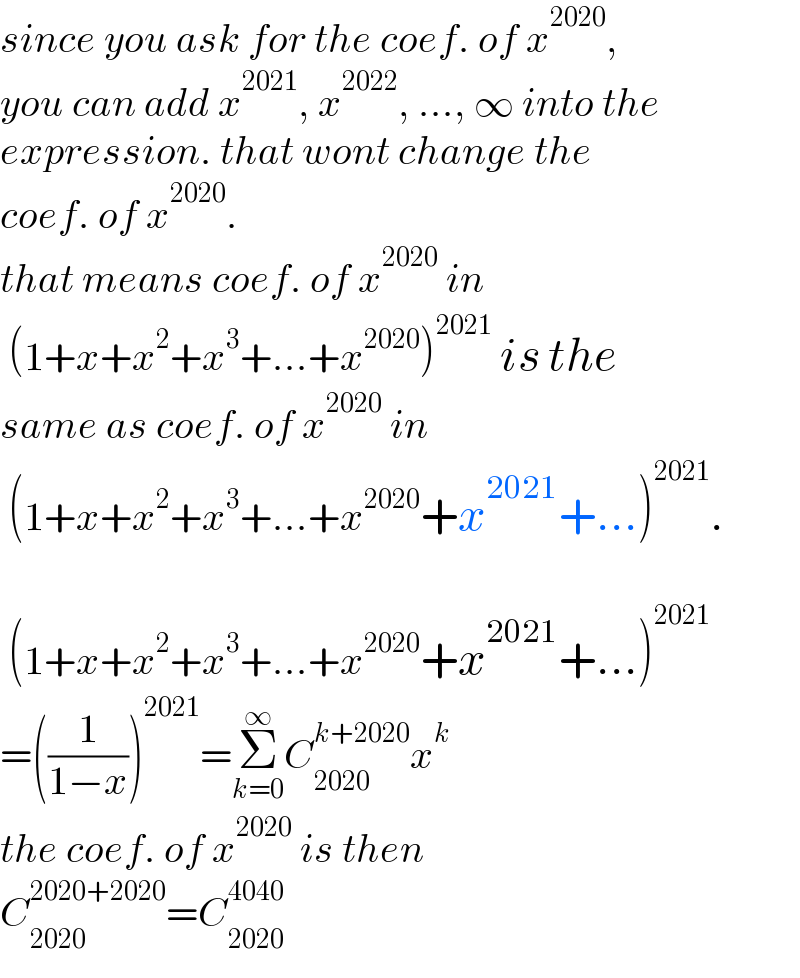
Commented by mr W last updated on 08/Jan/22
![but if you ask for the coef. of x^(2050) , then you must proceed normally as following. (1+x+x^2 +x^3 +...+x^(2020) )^(2021) =[((1−x^(2021) )/(1−x))]^(2021) =(1−x^(2021) )^(2021) Σ_(k=0) ^∞ C_k ^(k+2020) x^k coef. of x^(2020) is C_(2020) ^(2020+2020) coef. of x^(2050) is C_(2050) ^(2050+2020) −2021C_(29) ^(29+2020)](https://www.tinkutara.com/question/Q163596.png)
$${but}\:{if}\:{you}\:{ask}\:{for}\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{2050}} ,\: \\ $$$${then}\:{you}\:{must}\:{proceed}\:{normally} \\ $$$${as}\:{following}. \\ $$$$\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…+{x}^{\mathrm{2020}} \right)^{\mathrm{2021}} \\ $$$$=\left[\frac{\mathrm{1}−{x}^{\mathrm{2021}} }{\mathrm{1}−{x}}\right]^{\mathrm{2021}} =\left(\mathrm{1}−{x}^{\mathrm{2021}} \right)^{\mathrm{2021}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{k}} ^{{k}+\mathrm{2020}} {x}^{{k}} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{2020}} \:{is}\:{C}_{\mathrm{2020}} ^{\mathrm{2020}+\mathrm{2020}} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{2050}} \:{is}\:{C}_{\mathrm{2050}} ^{\mathrm{2050}+\mathrm{2020}} −\mathrm{2021}{C}_{\mathrm{29}} ^{\mathrm{29}+\mathrm{2020}} \\ $$
Commented by Tawa11 last updated on 08/Jan/22
$$\mathrm{Great}\:\mathrm{sir} \\ $$